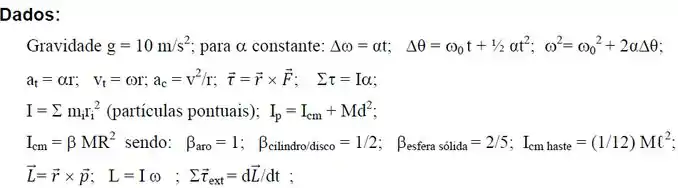
No instante de tempo um objeto esférico de massa e raio , gira deslizando com velocidade angular e velocidade do centro de massa nula em uma superfície horizontal com coeficiente de atrito cinético (veja a figura). Considere como ponto de contato do objeto com a superfície a origem do sistema de coordenadas. Utilize para a aceleração da gravidade.
a) Faça um diagrama de corpo livre do objeto.
b) Escreva as equações de Newton que descrevem o movimento.
c) Determine, enquanto o objeto rola deslizando, aceleração do seu centro de massa e sua aceleração angular .
d) Escreva as expressões em função do tempo para a velocidade do centro de massa e para a velocidade angular 𝜔(𝑡) do objeto enquanto ele rola deslizando.
e) Sabendo que no tempo o objeto esférico passa a rolar sem deslizar, ache a razão entre suas energias cinéticas de translação e rotação.
Passo 1
a)
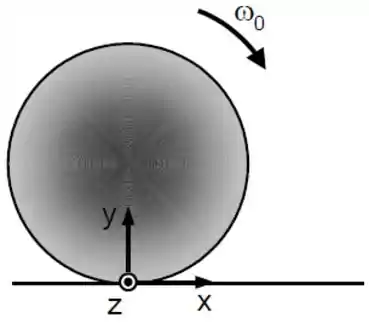
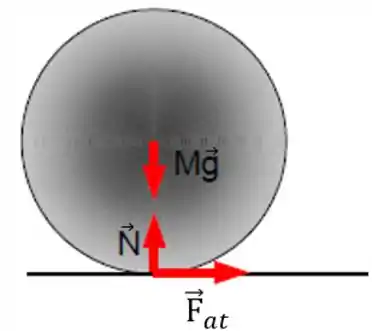
Esse é aquele típico primeiro item pra ninguém zerar a questão haha. As forças que atuam no objeto são a força peso , a força normal e a força de atrito , então o diagrama de corpo livre seria esse:
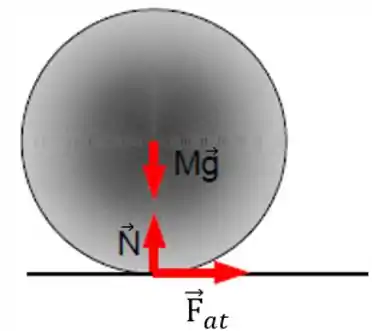
Só não tem que dar mole e botar, por costume, a força de atrito apontando pra esquerda! Porque a esfera está rodando no sentido horário, então o atrito tem que ser contra o movimento, no sentido anti-horário.
Passo 2
b)
Agora ele pediu as equações de Newton do movimento. Bem, temos uma mistura de uma translação com uma rotação. Vamos começar analisando a translação, beleza?
A translação é toda no eixo : a aceleração do objeto no eixo é nula. E pela 2ª lei de Newton,
Ou seja,
Portanto, o somatório das forças atuando no eixo , que são o peso e a normal, dá zero:
Passo 3
Show, agora vamos ver no eixo . Só temos a força de atrito atuando:
Então pela 2ª lei de Newton:
sendo o vetor aceleração do centro de massa do objeto.
Usando os módulos, também podemos escrever
Passo 4
Faltou só a rotação! O eixo de rotação é o centro da esfera, onde fica seu centro de massa. Repare que a única força realizando torque em relação a esse eixo é a força de atrito.
Portanto, o torque resultante em relação ao eixo passando pelo centro da esfera é igual ao torque realizado pela força de atrito:
E é dado por:
o vetor sendo o vetor posição do ponto de aplicação da força de atrito em relação ao centro da esfera.
Passo 5
Pela figura abaixo, podemos ver que :
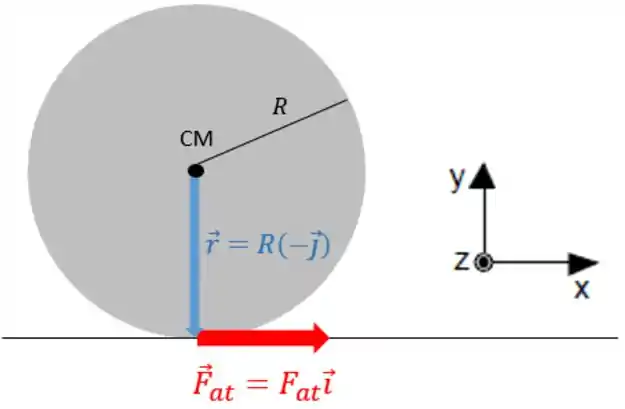
Ou seja,
E pela versão pra rotação da 2ª lei de Newton, sabemos que
Portanto, obtemos disso tudo que
O que, em módulo, fica:
Obs: Nem precisamos calcular o momento de inércia, ele só pediu pra montar as equações!
Passo 6
Recapitulando, usando as equações com os módulos, obtivemos:
Passo 7
c)
Agora queremos achar a aceleração do centro de massa e a aceleração angular .
Essa foi a que eu chamei simplesmente de no item anterior. E a gente achou
Ou seja, dá no mesmo dizer que
Passo 8
E o módulo da força de atrito a gente sabe calcular!
Vimos no item anterior que . Ou seja,
E a força de atrito aponta no sentido positivo do eixo , então
Passo 9
Agora ficou fácil!
Passo 10
Vamos partir pra aceleração angular! Na letra (b) vimos que
Depois também achamos
Ou seja,
Passo 11
Você pode até saber o momento de inércia de uma esfera, mas de qualquer maneira o enunciado dá:
Portanto,
Então a equação de cima fica
Passo 12
Mas a gente quer o vetor . Vimos lá atrás que . Isso significa que tem o mesmo sentido do vetor .
Logo,
Passo 13
d)
Acabamos de achar que
Isso significa que a aceleração do centro de massa é constante, então a esfera está seguindo um MRUV, cuja equação pra velocidade é:
ou seja:
O enunciado diz que a velocidade inicial do centro de massa é nula, portanto:
Passo 14
Usando o mesmo raciocínio pra rotação, temos que a aceleração angular é constante:
E a equação o movimento circular uniformemente variado é:
Mas atenção! O sentido positivo da rotação é anti-horário e está no sentido horário! Então pra equação ser de uma rotação no sentido anti-horário, temos que inverter o sinal de , ok? Então vai ficar:
Passo 15
e)
Vejamos, ele disse que a esfera passou a rolar sem deslizar. Isso significa que o ponto de contato da esfera com o chão passa a ter velocidade nula. Ou seja, o atrito cinético vira um atrito estático, então a aceleração do CM vai ser alterada!
E ele pede a razão das energias cinéticas de translação e rotação exatamente no momento em que a esfera passa a rolar sem deslizar. Mas essa mudança é instantânea, no momento as equações do movimento que achamos na letra (d) ainda estão valendo!
Acho que esse lance da esfera passar a rolar sem deslizar era uma tentativa de pegadinha do enunciado (que, diga-se de passagem, é meio confuso).
Enfim, não vamos nos preocupar com isso e podemos usar na maior tranquilidade os valores:
Passo 16
A energia cinética de translação é:
Passo 17
E a energia cinética de rotação é:
Vou deixar assim pra poder cortar esse com o do .
Passo 18
Show, estamos quase acabando! A razão das energias cinéticas é:
Vai dar pra cortar um monte de coisa, saca:
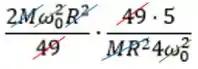
Então sobrou:
Resposta
a)
b)
c)
d)
e)