Na figura abaixo observa-se uma barra fina uniforme no plano horizontal de massa desprezível e comprimento . Ela está inicialmente em repouso e presa a um eixo que passa pelo seu centro de massa e aponta na direção . Este eixo pode girar livremente. Duas partículas de massa 𝑚 e 2𝑚 se movimentam paralelamente com velocidade 𝑣 na direção () e vão se chocar simultaneamente com a barra nas suas extremidades, como mostra a figura. Após a colisão as partículas ficam grudadas na barra.

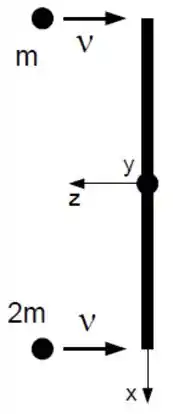
O módulo da velocidade angular do sistema logo após a colisão é igual a:

(a)

(b)

(c)

(d)

(e) 𝐴 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑡𝑜𝑡𝑎𝑙𝑚𝑒𝑛𝑡𝑒 𝑖𝑛𝑒𝑙á𝑠𝑡𝑖𝑐𝑎, 𝑝𝑜𝑟𝑡𝑎𝑛𝑡𝑜 𝑎 𝑣𝑒𝑙𝑜𝑐𝑖𝑑𝑎𝑑𝑒 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑎𝑝ó𝑠 𝑎 𝑐𝑜𝑙𝑖𝑠ã𝑜 é 𝑧𝑒𝑟𝑜.

Vamos dar uma olhada no momento angular total inicial!

A barra tem massa desprezível, então ela não tem momento angular. Portanto, o momento angular total do sistema é a soma dos momentos angulares das 2 partículas!

Cada uma delas tem seu vetor posição, sua massa e seu vetor velocidade, então é melhor tratá-las separadamente. Vou chamar a partícula de cima (de massa ) de partícula 1 e a outra, de massa , de partícula 2, beleza?

Vamos começar pela partícula 1!

Ela se choca na parte de cima da barra, a uma distância do centro da barra (que é a origem), no sentido negativo do eixo . Então sendo o vetor unitário do eixo , temos

E pelo enunciado, sabemos que a massa da partícula 1 é e que seu vetor velocidade é .

Ou seja o momento linear inicial da partícula 1 é:

Vamos usar o mesmo raciocínio pra partícula 2! Ela também se choca a uma distância do centro de massa, mas é no sentido positivo do eixo ! Ou seja,

A massa da partícula 2 é e seu vetor velocidade é . Portanto, seu momento linear inicial é:

Isso significa que o momento linear inicial do sistema é:

Então o momento angular final do sistema tem que dar isso também!

Depois da colisão a gente não sabe mais a velocidade das partículas, só é dito que elas ficam grudadas na barra. Então pra calcular o momento angular é melhor usar a fórmula

até porque a gente quer achar o módulo da velocidade angular .

Então vamos calcular o momento de inércia da barra, com as partículas grudadas nas extremidades!

Na verdade isso vai ser tranquilo porque a barra tem massa desprezível. Então só precisamos considerar as massas das partículas. E o momento de inércia de uma partícula em relação a um eixo é:

A partícula 1 tem massa , a partícula 2 tem massa e ambas estão a uma distância do eixo, portanto:

Ou seja, o momento angular final do sistema é:

Portanto, pela conservação do momento angular total:

Vamos dar uma ajeitada nisso pra achar o ! Cortando dos 2 lados, fica:

E ele pediu o módulo da velocidade angular, então: