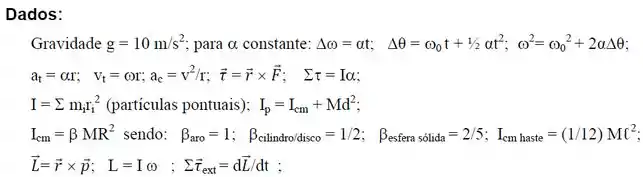
Uma esfera de massa 4,0 𝑘𝑔 e um cubo de massa 2,0 𝑘𝑔 estão conectados por uma corda inextensível e de massa de desprezível. A corda passa por uma roldana de raio 1,0 𝑚 e massa 2,0 𝑘𝑔 que tem a forma de um disco como ilustrado esquematicamente na figura ao lado. Ambos os corpos estão com velocidade de módulo igual a 𝑣 (𝑚/𝑠). Calcule em o módulo do momento angular do sistema em relação ao centro da roldana.
(a)
(b)
(c) 7
(d)
(e)
Passo 1
O sistema é composta de 3 partículas: o cubo, a roldana e a esfera. Então o momento angular total do sistema em relação ao centro da roldana é a soma dos momentos angulares das 3 partículas em relação ao centro da roldana.
E temos 2 maneiras de calcular o momento angular:
e
onde é o vetor posição, também chamado de braço da alavanca (que nem vimos pro torque!).
Passo 2
A roldana é um disco então seu momento de inércia é:
E como sua massa e seu raio são, respectivamente, e , isso dá:
Passo 3
Vamos calcular o momento angular do cubo em relação ao centro da roldana, usando a fórmula
O que, em módulo, dá:
Observando a figura com carinho, podemos ver que o braço da alavanca é o raio da roldana!
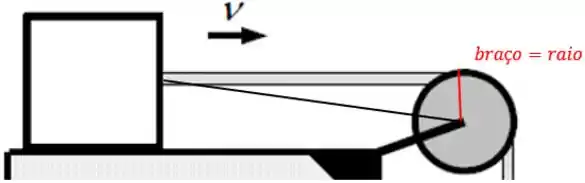
Ou seja,
E como a massa do cubo é , obtemos:
Passo 4
Agora vamos pro momento angular da roldana! Dessa vez vamos usar a fórmula
Ou, usando os módulos:
Temos
e já vimos que
Logo,
Passo 5
Beleza, agora só falta o momento angular da esfera!
Assim como pro cubo, o vetor , braço da alavanca, tem módulo :
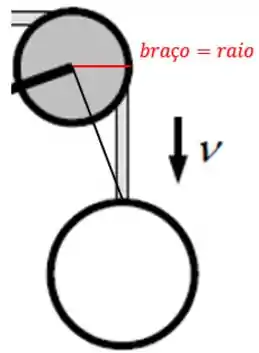
E como a esfera tem massa , o módulo do seu momento angular é:
Passo 6
Show! Então somando tudo:
Resposta
Alternativa (c)