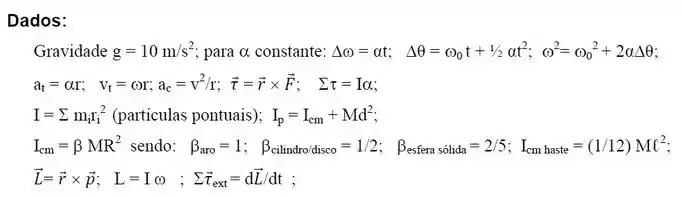
Na preparação para um salto com vara, o atleta ilustrado abaixo mantém a vara em equilíbrio estático na posição horizontal. Para isto ele faz numa extremidade da vara, posição A, uma força na vertical para baixo igual a e na posição B uma força na vertical para cima igual a . A vara tem comprimento igual a 5,0 𝑚 e massa 3,0 𝑘𝑔.
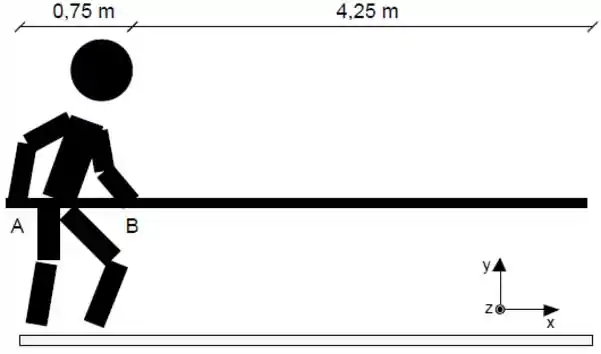
a) Calcule o momento de inércia rotacional da vara em relação ao eixo que passa pelo ponto B na direção do eixo .
b) Determine as forças e .
c) Suponha agora que em 𝑡 = 0 o atleta solte a vara na posição B e mantenha firme a posição A, de forma que a vara possa girar livremente em torno da posição A no plano em direção ao chão. Calcule o módulo da aceleração angular da barra neste instante.
d) Calcule a velocidade angular da barra quando o deslocamento angular for igual a .
Passo 1
a)
Não se confunda com o “rotacional”, basicamente o que ele pediu é o momento de inércia da barra em relação ao eixo que passa pelo ponto B na direção do eixo .
Parece uma boa pedida pra usar o teorema dos eixos paralelos, né?? :)
Passo 2
Primeiro precisamos do momento de inércia da barra em relação ao eixo que passa pelo seu centro. E isso, se você não souber...não faz problema! Pois é, ele dá nos dados
A vara é a haste, com massa e comprimento . Logo,
Passo 3
Show, agora é só aplicar o teorema dos eixos paralelos!
sendo a distância entre o centro da vara e o ponto B. A vara tem metros, então o seu centro está a das extremidades. E o ponto B está a da extremidade esquerda. Ou seja, a distância é:
Passo 4
Substituindo na fórmula:
Passo 5
b)
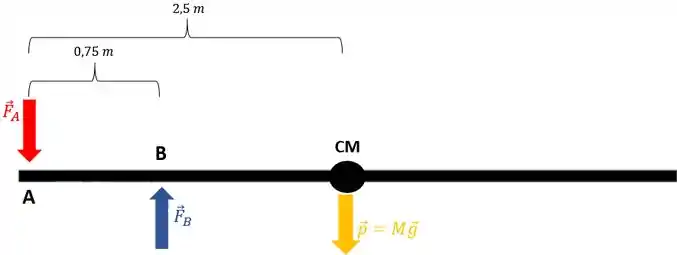
Agora queremos achar e , e pra isso uma boa é analisar todas as forças atuando na vara. Na verdade, além da e da , só tem a força peso . E ela atua bem no meio da vara, que é onde fica o centro de massa.
Passo 6
Temos 3 forças capazes de realizar torque, por isso, por mais que a barra esteja em equilíbrio, temos uma dinâmica de rotação. Vamos considerar o eixo passando pelo ponto A como eixo de rotação da vara.
Obs: Poderíamos escolher qualquer ponto da barra, mas é bom pegar um onde uma força está sendo aplicada, além do mais se for uma força que a gente quer achar!
Enfim, isso significa que a força está sendo aplicada diretamente no eixo de rotação, então o torque dela é nulo!
Passo 7
E a barra está em equilíbrio, portanto o torque no sentido horário e o torque no sentido anti-horário se cancelam!
E olhando a figura, podemos ver que realiza torque no sentido horário, enquanto o torque da é no sentido anti-horário (tudo isso em relação a A).
Ou, em módulo:
Por mais que a gente queira achar as forças vetoriais, é mais fácil fazer as contas com os módulos e depois voltar pra vetor, tranquilo?
Passo 8
Lembrando que
Então vamos calcular o módulo desses torques! Temos que multiplicar a distância ao eixo de rotação (ponto A) pelo módulo da força:
Como e :
Passo 9
Show, então voltando pro que achamos antes:
Agora vamos voltar pra forma vetorial. Sabemos que é pra cima, no sentido do eixo , portanto:
Passo 10
Ok, agora só falta achar a . Pra isso, vamos deixar a rotação de lado e voltar à nossa boa e velha análise de forças :)
A vara está em equilíbrio, então o somatório de forças nela dá zero:
e então:
Passo 11
c)
Agora o atleta soltou a vara na posição B e manteve firme a posição A onde estava. E o enunciado pediu o módulo da aceleração angular da vara. Parece ideal pra gente usar a relação entre torque resultante e aceleração angular:
Se a rotação fosse em torno do centro de massa, o problema já estaria praticamente resolvido, mas ela é em torno do ponto A. Mas podemos adaptar a fórmula sem problemas pro ponto A:
Então temos que achar o momento de inercia da vara em relação a A!
Passo 12
Aplicando o teorema dos eixos paralelos:
onde é a distância entre o ponto A e o centro de massa, ou seja, .
E já achamos lá na letra (a) que . Então vamos ter
Passo 13
Ótimo! Então
E esse torque resultante dá pra gente achar! Já que não tem mais a , a única força realizando torque em relação ao ponto A é a força peso:
Agora é só partir pro abraço!
Passo 14
d)
Agora queremos a velocidade angular da barra quando o deslocamento angular for igual a . Seria mais ou menos assim:
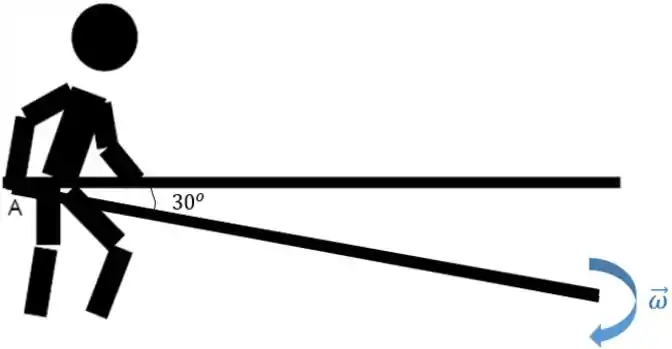
Ele falou porque são rodados no sentido horário, só isso! Então podemos botar mesmo :)
Passo 15
Com essa velocidade angular , a vara adquire uma energia cinética de rotação. Então podemos tentar aplicar a conservação da energia mecânica!
As únicas forças atuando são a força peso, que é conservativa, e a força de sustentação do atleta pra manter a barra no lugar. Essa força não faz o sistema perder energia, portanto ela também é conservativa! Então podemos aplicar a conservação da energia mecânica:
sendo a energia cinética e a energia potencial gravitacional.
É importante notar que o movimento é uma rotação pura, sem translação, então a energia cinética total é igual à energia cinética de rotação.
Passo 16
A energia cinética de rotação é dada por
No caso do exercício, a rotação é em relação ao ponto A, então:
E como eu disse antes, a energia cinética total é igual à energia cinética de rotação, portanto:
Substituindo isso dá:
Passo 17
Agora , antes de mais nada, temos que definir um zero de energia potencial gravitacional. Ela se escreve da forma . Então esse a gente tem que saber em relação ao quê vai ser! Seria bom a gente escolher algo que facilite as contas, dando por exemplo. Então vamos fazer isso!
Resta a saber qual vai ser a altura da barra na posição inicial, em relação a esse zero de energia potencial gravitacional.
Se ficou confuso relaxa que na figura tá bonitinho (eu espero!):
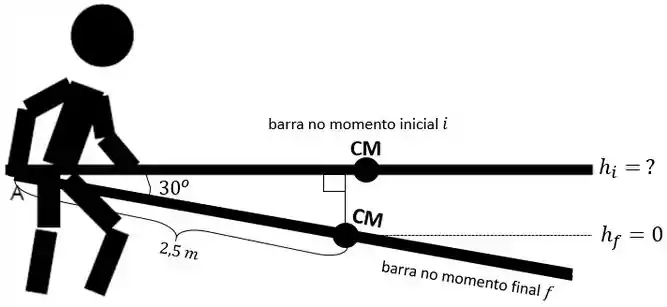
Passo 18
E pra gente achar esse vai ser um probleminha de trigonometria tranquilo! Saca só:
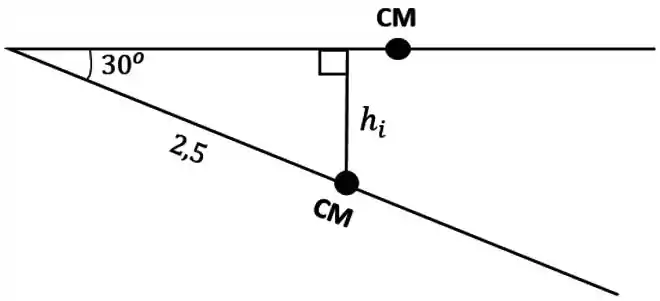
Ou seja,
Passo 19
Beleza, agora vamos voltar à conservação da energia mecânica:
E esse seria o módulo do vetor que o enunciado pediu.
Repare que a barra sai do repouso, no momento inicial sua velocidade angular é nula: . Também já vimos que: , , e . Então isso vai dar:
Como é o módulo de um vetor, ele é positivo, então
Passo 20
Calma que ainda não acabou! Queremos o vetor velocidade angular ! Mas isso vai ser tranquilo, basta lembrar 2 coisas:
- o vetor velocidade angular é ortogonal à rotação tem o sentido de ou
- o sentido considerado positivo é o sentido anti-horário
Como a nossa rotação é no sentido horário, o vetor velocidade angular aponta pra dentro do plano, na direção do vetor .
Ou seja,
Resposta
a)
b)
c)
d)