P3 de Física B - FIS1026 da PUCRIO - 2017.1

Duas massas e estão penduradas por fios inextensíveis e de massas desprezíveis a uma polia. A polia é formada por discos, ligados de maneira que formam um corpo único. Considere o momento de inércia total da polia em relação ao seu centro de massa como sendo . O fio ligado a está enrolado no disco externo de raio e o fio ligado a está enrolado no disco interno de raio . Despreze o atrito.

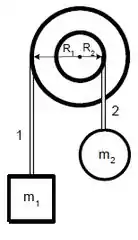
1. Escreva as equações de movimento (2ª Lei de Newton) para o sistema de forma que fosse possível determinar a aceleração angular da polia .
2. Suponha agora que e . Se , e , o sistema se encontra em equilíbrio estático. Calcule os torques e que os fios realizam sobre o corpo.

Escreva os torques primeiro em notação literal para então substituir os valores dados. Utilize o sistema de coordenadas indicado.

3. Suponha que uma massa de seja adicionada no topo da massa dada no item anterior e que o sistema entre em movimento. No instante de tempo em que a massa tiver alcançado em módulo uma velocidade , calcule o módulo da velocidade da massa neste mesmo instante.

Seja um corpo na forma de um formado por duas barras finas de comprimento e massa como ilustra a figura ao lado. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na vista frontal indicada .

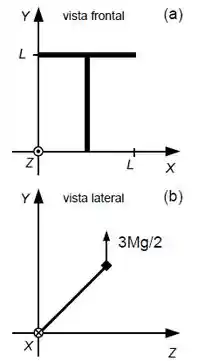
1. Determine o momento de inércia rotacional do corpo em torno do eixo e a posição do seu centro de massa na posição indicada na figura em função dos dados do problema.
2. O corpo é girado em torno do eixo e colocado na posição mostrada na vista lateral . O eixo positivo na vista lateral aponta para dentro do plano do papel. O corpo faz com o plano onde permanece em equilíbrio estático com a ajuda da força . Determine a força que o eixo faz no corpo nesta posição em função dos dados do problema.
3. Suponha agora que a força pare de atuar e que o corpo, a partir da posição do item anterior, passe a girar livremente em torno do eixo , partindo do repouso. Determine a energia cinética do copro quando ele cruzar o plano .

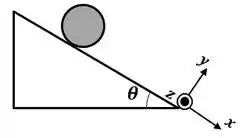
Um disco maciço de madeira de massa e raio rola para baixo sem deslizar em um plano rugoso de comprimento , inclinado de um ângulo em relação à horizontal. Utilize o sistema de coordenadas indicado.

1. Desenhe as forças que agem no disco durante o rolamento. Desenho no plano, se existirem, seus pares ação-reação.



2. Calcule o momento angular total do disco , em relação à origem do sistema de coordenadas, quando ele estiver no meio do plano e com velocidade do seu centro de massa ao longo do plano . Suponha que , e . Desenhe os vetores , e na figura abaixo.



3. O momento angular do disco, em relação à origem do sistema de coordenadas, ao longo da descida no plano inclinado é ou não é conservado? Por que?