Duas massas e estão penduradas por fios inextensíveis e de massas desprezíveis a uma polia. A polia é formada por discos, ligados de maneira que formam um corpo único. Considere o momento de inércia total da polia em relação ao seu centro de massa como sendo . O fio ligado a está enrolado no disco externo de raio e o fio ligado a está enrolado no disco interno de raio . Despreze o atrito.
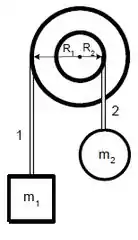
- Escreva as equações de movimento (2ª Lei de Newton) para o sistema de forma que fosse possível determinar a aceleração angular da polia .
- Suponha agora que e . Se , e , o sistema se encontra em equilíbrio estático. Calcule os torques e que os fios realizam sobre o corpo.
- Suponha que uma massa de seja adicionada no topo da massa dada no item anterior e que o sistema entre em movimento. No instante de tempo em que a massa tiver alcançado em módulo uma velocidade , calcule o módulo da velocidade da massa neste mesmo instante.
Escreva os torques primeiro em notação literal para então substituir os valores dados. Utilize o sistema de coordenadas indicado.
Passo 1
Letra a)
Antes de tudo nesse mundo, precisamos fazer o mais importante: Pensar em qual o nosso sistema de coordenadas. Como tudo só se move na vertical, só vou me preocupar com isso.
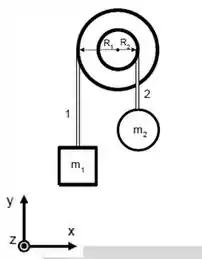
Onde eu defini a origem láaa no chão, mas só pra ninguém ficar encucado com isso, porque ela não importa muito.
Agora, precisamos escrever as equações do movimento para os bloquinhos, visto que os torques realizados na polia depende deles (o peso dos bloquinhos é transmitido pra polia pelas cordas)

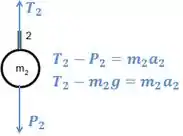
Como os fios se enrolam em polias de tamanhos diferentes, o comprimento deles não se relacionam diretamente, e logo .
Passo 2
Pronto, agora vamos para a polia e a versão angular da segunda lei de newton, que diz que:
Onde é o torque resultante. Vamos olhar as forças nas polias.
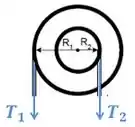
Eu omiti o peso da polia, porque ele não realiza torque sobre ela (e tirando a sua incrível capacidade de girar, a polia está fixa, então nada de polia caindo).
Como as reações de e fazem com a distância ao centro das polias, o torque de cada uma é o produto da tensão com o raio.
Porém, cada força faz a polia girar pra lados diferentes. Assim, temos:
Um último comentário: a aceleração angular é a mesma para as duas partes da polia! A cinemática de rotação daria que:
Passo 3
Letra b)
Neste item, o sistema se encontra em equilíbrio estático. Logo:
Já para saber os torques: No item anterior, nós pulamos o produto vetorial e fomos direto pra sua forma com seno (). Dessa vez, vamos pensar um pouco nele.
O sentido de é o negativo do eixo , enquanto o de é o negativo do eixo . Usando a regra da mão direita, a direção do torque é no eixo enquanto os dois negativos se cancelam, e aponta na direção positiva do eixo .
Já para , também está no sentido negativo de , mas está no sentido positivo de . Logo:
Do enunciado:
(o último não estava no enunciado, mas a gente praticamente sempre aproxima assim, e nesse caso tava na prova).
Substituindo, temos:
Passo 4
Letra c)
Podemos relacionar a velocidade angular das polias com a velocidade linear de cada bloquinho. De fato, temos:
Se , então usando os dados do item anterior as polias terão uma velocidade angular:
Substituindo na segunda equação:
Sendo e o módulo das velocidades dos bloquinhos. Porque de fato, o sentido dos dois será opostos.
Resposta
Letra a)
Letra b)
Letra c)