Seja um corpo na forma de um formado por duas barras finas de comprimento e massa como ilustra a figura ao lado. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na vista frontal indicada .
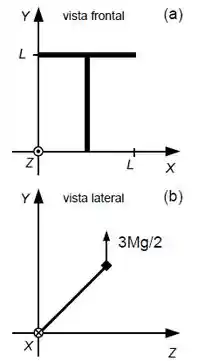
- Determine o momento de inércia rotacional do corpo em torno do eixo e a posição do seu centro de massa na posição indicada na figura em função dos dados do problema.
- O corpo é girado em torno do eixo e colocado na posição mostrada na vista lateral . O eixo positivo na vista lateral aponta para dentro do plano do papel. O corpo faz com o plano onde permanece em equilíbrio estático com a ajuda da força . Determine a força que o eixo faz no corpo nesta posição em função dos dados do problema.
- Suponha agora que a força pare de atuar e que o corpo, a partir da posição do item anterior, passe a girar livremente em torno do eixo , partindo do repouso. Determine a energia cinética do copro quando ele cruzar o plano .
Passo 1
Letra a)
O momento de inércia vai ser dado por:
Onde é a distância de cada elemento de massa até o eixo de rotação. A integral é “só” um somatório de todos esses termos.
Mas se ela é uma soma de todos esses pedacinhos , não faz diferença se eu quiser separar a integral e somar primeiro os da barra vertical e depois os da barra horizontal.
Então é exatamente isso que eu vou fazer.
Então vamos agora observar o momento de inércia de cada barrinha.
Passo 2
Para a barrinha vertical, nós conhecemos o seu momento de inércia ao redor do seu meio (onde fica o seu centro de massa). Vamos então ter que usar o teorema dos eixos paralelos.
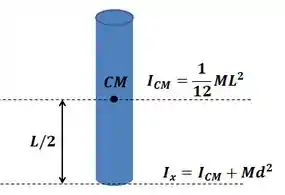
O seu momento de inércia ao redor do eixo fica:
Já para a barrinha vertical, teremos:
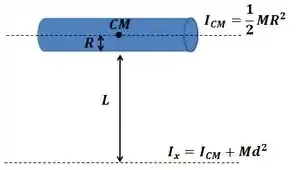
Nota que o enunciado não deu o raio da barra. Então vamos desistir do problema e partir pro próximo? NUNCA!
Ele não diz , mas ele diz: “um corpo na forma de um formado por duas barras finas”. Se as barras são “finas”, o raio delas é praticamente desprezível frente ao comprimento delas. Assim, se fizermos o limite , teremos:
O momento de inércia da forma fica:
Passo 3
Pra fechar a letra , vamos agora encontrar a posição do seu centro de massa. O centro de massa de um sistema de partículas tem componentes dadas por:
Porém, como temos duas barrinhas juntas, podemos imaginar como se fossem duas partículas de massa , cujas posições são as posições de seus centros de massa (que ficam exatamente no meio da barra).
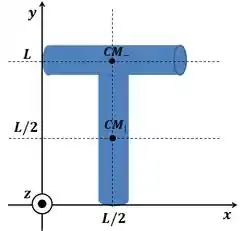
Assim:
Onde levamos em conta que temos duas barras de massa , logo uma forma de massa .
Assim, o vetor posição do centro de massa da nossa forma fica:
Passo 4
Letra b)
As condições para termos equilíbrio estático são:
Se usarmos a primeira condição com as forças dadas teremos:
Rearrumando:
Passo 5
Letra c)
Quando o corpo começar a girar, o que temos é a sua energia potencial gravitacional se tornando energia cinética (tanto de translação do centro de massa quanto de rotação do corpo extenso).
Como o que queremos é de fato a energia cinética, então esse é um problema de conservação da energia.
Inicialmente, o sistema está em repouso, logo . No fim, o sistema atinge o plano , onde , que vamos tomar como a referência para a energia potencial gravitacional. Por isso, . Temos então:
A energia potencial gravitacional inicial é do centro de massa.
Para acharmos a altura do centro de massa, usamos um pouco de geometria.
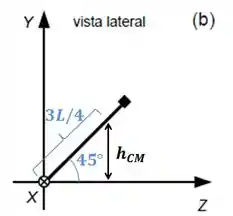
O motivo da distância da ponta do “T” até o centro de massa ser são os itens que fizemos antes. Neles, quando consideramos que , nós assumimos (tava meio escondido no raciocínio) que a barra estava paralela ao eixo (se não fosse o caso, como estamos vendo aqui, teríamos invés de ).
Ou seja, significava a distância da ponta da forma até o centro de massa.
Agora, podemos usar nossa amiga trigonometria:
Substituindo lá em cima:
Assim, pela conservação da energia (e simplificando esse rapaz aí)
Nota que o problema pediu a “energia cinética”, ou seja, a energia cinética total (translação do centro de massa somada à translação).
Resposta
Letra a)
Letra b)
Letra c)