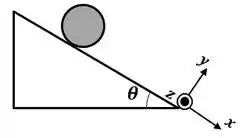
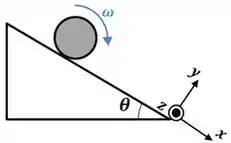
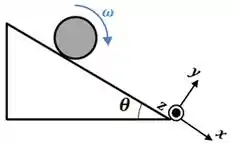
Um disco maciço de madeira de massa e raio rola para baixo sem deslizar em um plano rugoso de comprimento , inclinado de um ângulo em relação à horizontal. Utilize o sistema de coordenadas indicado.
- Desenhe as forças que agem no disco durante o rolamento. Desenho no plano, se existirem, seus pares ação-reação.
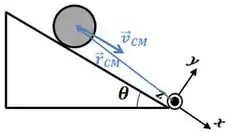
- Calcule o momento angular total do disco , em relação à origem do sistema de coordenadas, quando ele estiver no meio do plano e com velocidade do seu centro de massa ao longo do plano . Suponha que , e . Desenhe os vetores , e na figura abaixo.
- O momento angular do disco, em relação à origem do sistema de coordenadas, ao longo da descida no plano inclinado é ou não é conservado? Por que?
Passo 1
Letra a)
Ok, vamos fazer desenhinhos.
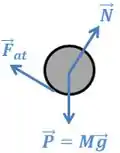
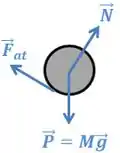
A força que atua na bola é a normal que o plano exerce sobre ela, enquanto é o peso da bola. Como o plano é rugoso, também temos uma força de atrito , realizada do plano sobre a bola (afinal, ela é devida à rugosidade do plano).
A normal é sempre perpendicular à superfície de contato, enquanto o peso está sempre em direção ao centro da Terra. Já a força de atrito se opõe ao movimento.
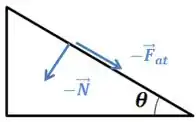
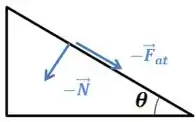
Já no plano, teremos os pares de reação que a bola exerce nele. Como apenas duas das forças que falamos antes são causadas pelo plano, apenas elas terão um par de reação ( e ).
Passo 2
Letra b)
O momento angular total de um sistema de partículas ao redor de um ponto qualquer pode ser decomposto como:
Onde é o momento angular do centro de massa com relação a e é o momento angular de todo o corpo em relação ao centro de massa.
O módulo do momento angular ao redor do centro de massa fica:
Onde eu já substitui logo o momento de inércia de um disco.
Como o disco gira no sentido horário, o vetor velocidade angular vai ser no sentido negativo do eixo (eixo de rotação).
Então o momento angular em relação ao centro de massa ficaria:
Agora fica faltando o do centro de massa.
Passo 3
Neste caso, temos:
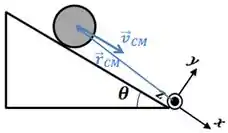
No sistema de coordenadas dado, teremos que:
Precisamos então saber onde está o centro de massa. Para isso, vamos observar suas componentes.
Ao longo do eixo , ele está na metade da rampa.
Ao longo do eixo , ele está a uma “altura” igual ao raio do disco.
Como a origem está na frente do disco rodando, teremos:
Assim:
No produto vetorial, vale o que chamamos de “distributiva”:
Como e são paralelos (ou “antiparalelos”), o seu produto vetorial zera. Além disso, como é o vetor unitário ao longo do eixo e é ao longo do eixo , pela regra da mão direita temos:
Agora, finalmente, juntando tudo:
Passo 4
O momento angular total vai ser:
Pela cinemática angular, temos que , e todos os pontos teram a velocidade linear do centro de massa, logo . (Isso é porque é como se o centro de massa o dono do movimento linear).
Pelo enunciado:
Passo 5
Letra c)
Temos três forças que atuam no disco: , e .
- é sempre perpendicular ao movimento do centro de massa e orientada ao longo do raio do disco. Logo, ele não causa torque.
- também está orientada ao longo do raio do disco, e por isso não causa um torque.
Se ninguém gera torque, como o disco gira?! Bem, só sobrou , que de fato gera torque (atua na parte “debaixo” do disco orientado ao longo do movimento, no sentido oposto).
Temos então que o momento angular não se conserva devido ao atrito (afinal, o torque resultante é igual à variação do momento angular com o tempo).
Resposta
Letra a)
Letra b)
Letra c)
O momento angular não se conserva.