P3 de Física B - FIS1026 da PUCRIO - 2018.2

O objeto ilustrado na figura ao lado pode girar livre em torno do eixo fixo . Ele é composto 6 por hastes finas. As 2 hastes ao longo dos eixos e têm, cada uma, comprimento e massa e estão presas pelo seu seu centro de massa ao eixo de rotação. As 4 hastes inclinadas têm, cada uma, a mesma massa . Em determinado instante , a força de módulo na direção horizontal é aplicada no ponto conforme mostra a figura. No mesmo instante, outra força de módulo e com a inclinação igual a inclinação da haste é aplicada no ponto .

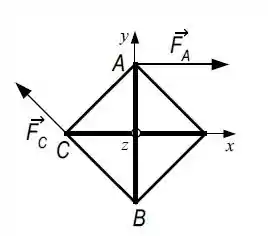
a) Mostre que o momento de inércia do objeto em torno do eixo é dado por .

b) Escreva os vetores e necessários para calcular o torque em torno do eixo provocado pela força aplicada em , em . Calcule o produto vetorial e encontre .

c) Calcule o torque em torno do eixo provocado pela força aplicada em , em .

d) Calcule a aceleração angular do objeto neste instante.

e) Suponha agora que, para impedir o objeto de girar, uma terceira força é aplicada na direção horizontal no ponto , em . Determine esta forca .

f) Se ao invés da força aplicada no item anterior, a força em B for . Calcule a força que o eixo faz no objeto para que este fique em equilíbrio estático.

Seja um plano inclinado de um ângulo com a horizontal, com coeficientes de atrito cinético e estático iguais a e , respectivamente. No seu topo, um objeto de massa é mantido em repouso através de um freio. Ele está conectado a um cabo que passa por uma roldana e que está preso a uma mola na vertical de constante elástica desconhecida. A outra extremidade da mola está presa ao solo. Nesta situação a mola está relaxada. Quando o freio é retirado, o objeto desliza plano abaixo uma distância até ser parado pela força da mola esticada.

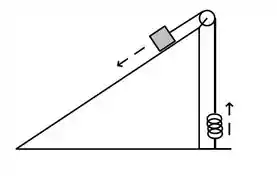
Considerem o cabo, a roldana e a mola sem massa e ideais. Responda em função dos dados do problema.

a) Determine a variação da energia cinética do objeto do início ao final do trajeto.

b) Determine a variação da energia potencial gravitacional do objeto do início ao final do trajeto.

c) Determine o trabalho realizado pelo atrito do início ao final do trajeto.

d) Escreva para esta situação específica a equação de conservação de energia apropriada.

e) Determine a energia potencial elástica armazenada na mola ao final do trajeto.

A haste de comprimento e massa está livre para girar em torno de um pino fixo na direção do eixo 𝑧. A haste é largada do repouso na posição horizontal e quando chega na posição vertical, sua extremidade inferior colide na altura do centro de massa de um disco de massa e raio . Ele está em repouso sobre uma superfície horizontal com coeficientes de atrito cinético e estático iguais a e respectivamente. Ao final do trajeto a superfície se inclina com um ângulo em relação à horizontal.

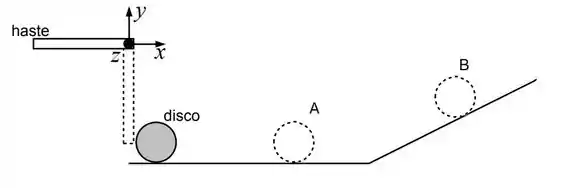
a) Quando a haste chega na posição vertical, imediatamente antes da colisão, sua velocidade na extremidade é . Imediatamente após a colisão o disco tem movimento só de translação com velocidade linear Determine a velocidade linear na extremidade da haste imediatamente após a colisão.

b) Após o deslizamento inicial, o disco passa a rolar sem deslizar ao longo da superfície horizontal com velocidade linear no centro de massa constante . Determine a energia cinética do disco.

c) Desenhe na figura acima todas as forças que agem sobre o disco enquanto ele rola sem deslizar na superfície horizontal (posição A) e enquanto ele sobe a superfície inclinada também rolando sem deslizar (posição B).

d) Determine a altura máxima que o disco alcança em relação à base da superfície inclinada. Justifique sua resposta.