Seja um plano inclinado de um ângulo com a horizontal, com coeficientes de atrito cinético e estático iguais a e , respectivamente. No seu topo, um objeto de massa é mantido em repouso através de um freio. Ele está conectado a um cabo que passa por uma roldana e que está preso a uma mola na vertical de constante elástica desconhecida. A outra extremidade da mola está presa ao solo. Nesta situação a mola está relaxada. Quando o freio é retirado, o objeto desliza plano abaixo uma distância até ser parado pela força da mola esticada.
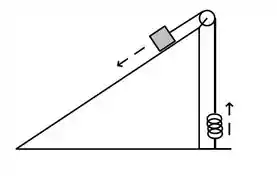
Considerem o cabo, a roldana e a mola sem massa e ideais. Responda em função dos dados do problema.
a) Determine a variação da energia cinética do objeto do início ao final do trajeto.
b) Determine a variação da energia potencial gravitacional do objeto do início ao final do trajeto.
c) Determine o trabalho realizado pelo atrito do início ao final do trajeto.
d) Escreva para esta situação específica a equação de conservação de energia apropriada.
e) Determine a energia potencial elástica armazenada na mola ao final do trajeto.
Passo 1
Tem um bloquinho que está com um freio (finge que é esse triâgulo em vermelho), ele tá impedindo o bloco de descer..Então é mais ou menos isso aí que está na figura 1.
Aí em um certo momento eles tiram o triângulo e o bloco desce e, consequentemente, o fio que tava preso no bloco puxa a mola, como mostra a figura 2:
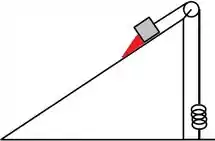
Figura 1Figura 2
Beleza, entendemos o que acontece nesse processo...Vamos ver o que a letra a tá pedindo.
Passo 2
a)Avariação da energia cinética entre aqueles dois pontos lá que eu mostei nas figuras 1 e 2. Naqueles pontos, qual é a velocidade do bloquinho?
Olha, no início, tem o freio então ele tá parado, logo: . Então
Na figura dois o bloquinho tá parado, porque a mola tá segurando ele. Olha lá no enunciado, ele fala pra gente que o bloquinho parou, por isso
Logo,
Passo 3
b) Agora a gente quer saber .
Mas quais são os valores dessas alturas? É ? Não!! Olha só quem é o e quem são as alturas:
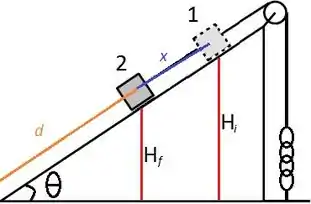
Maravilha, esse d que está ali eu inventei... só para dar um nome para aquele comprimento, porque vamos precisar dele para achar as alturas. Porque nós temos dois triângulos retângulos ali. Então calculando o para os dois ttriângulos:
e
Isolando o e o , e substituindo os valores lá na equação da energia potencial, a gente fica com:
Show de bola? Show of ball! Agora calculando a variação:
Viu como o d nem apareceu na resposta! Foi só para ajudar mesmo, mas como ele não é dado do problema, não pode aparecer na resposta!
Passo 4
c)
Ele tá querendo o trabalho que a faz no processo. O trabalho é o produto escalar entre a força e o deslocamento, mas relaxa...não é difícil...é essa relação:
Esse é o ângulo entre a força e o deslocamento. Então o que a gente tem que saber é para
onde a força, nesse caso a , tá apontando.Vamos fazer o diagrama de forças para o bloco:
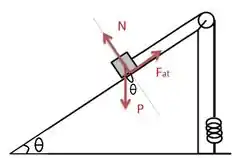
Como o deslocamento é pra baixo, o atrito tá pra cima, logo eles estão em sentido opostos. Assim, . Lembrando que e o deslocamento vale :
Pronto! É isso aí.
Passo 5
d)
Quando você pensar em conservação de energia, faz a seguinte pergunta: “Tem alguma força dissipativa roubando energia do nosso sistema?”
E aí?
Tem?
A é uma força dissipativa e tá realizando trabalho (como a gente viu na letra c), então a tá roubando energia do sistema...Logo a energia mecância do final não é igual a energia mecânica inicial, e a diferença entre esses valores é essa energia que a roubou. Sacou?
O bloco se movimenta, então tem . Ele muda de altura, então tem . Ele estica uma mola, então tem .
Passo 6
Ele tá pedindo a energia elástica no final do processo, ou seja, ele quer que a gente encontre . Com a equação quea gente montou na letra d fica moleza, acompanha comigo:
A gente viu na letra a que .
Vimos na letra b que
Vimos na letra c que
E como no início, já temos o freio, a mola não ta nem comprimida nem esticada, então .
Então:
Só sucesso!
Passo 7
Resposta
a)
b)
c)
d)
e)