O objeto ilustrado na figura ao lado pode girar livre em torno do eixo fixo . Ele é composto 6 por hastes finas. As 2 hastes ao longo dos eixos e têm, cada uma, comprimento e massa e estão presas pelo seu seu centro de massa ao eixo de rotação. As 4 hastes inclinadas têm, cada uma, a mesma massa . Em determinado instante , a força de módulo na direção horizontal é aplicada no ponto conforme mostra a figura. No mesmo instante, outra força de módulo e com a inclinação igual a inclinação da haste é aplicada no ponto .

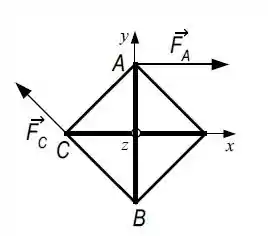
a) Mostre que o momento de inércia do objeto em torno do eixo é dado por .

b) Escreva os vetores e necessários para calcular o torque em torno do eixo provocado pela força aplicada em , em . Calcule o produto vetorial e encontre .

c) Calcule o torque em torno do eixo provocado pela força aplicada em , em .

d) Calcule a aceleração angular do objeto neste instante.

e) Suponha agora que, para impedir o objeto de girar, uma terceira força é aplicada na direção horizontal no ponto , em . Determine esta forca .

f) Se ao invés da força aplicada no item anterior, a força em B for . Calcule a força que o eixo faz no objeto para que este fique em equilíbrio estático.

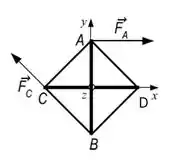
O momento de inércia das barras maiores, AB e CD, são iguais porque elas têm mesma massa M e comprimento 2L. O eixo passa pelo centro de massa, então a gente calcula assim:

Esses foram tranquilos, né? Vamos ver as outras hastes agora!

Essas outras hastes são diferentes, certo? Porque o eixo de rotação não passa no centro de massa delas. Aí a gente não pode usar a fórmula conhecida .Mas sem desespero...A gente ajeita isso daí rapidinho com o Teorema dos Eixos Paralelos.

Lembrando que esse d é a distância entre o centro de massa da haste e o nosso eixo de rotação z.

Olha, destaquei no desenho o d:

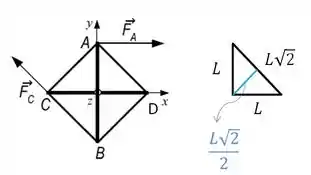
Olha que showww: Todas as hastes pequenas (AD, DB, BC e CA) estão a mesma distância do eixo de rotação. Então esse vale pra todo mundo.

Olha que show ainda mais: todas as barras pequenas tem mesma massa M e mesmo comprimento L. Então o momento de inércia delas são iguais.

Maravilha, vamos usar o teorema dos eixos paralelos e descobrir o de uma dessas hastes, aí já vai ser igual ao das outras:

Pronto! Agora já podemos descobrir o .

b)

Agora queremos calcular o torque causado pela força C.

O é o vetor do eixo de rotação até o ponto de aplicação da força. Então, quem é esse vetor?

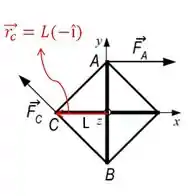
Maravilha! Vamos ver quem é a .

Ih caramba..Ela está meio inclinada. Vamos ter que decompor em suas componentes nos eixos x e y.

Pô..vou ter que pensar em ângulo ainda?

Olha só, isso ele “deu” pra gente. Porque todas as hastes tem o mesmo comprimento L. Então o objeto é quadrado.

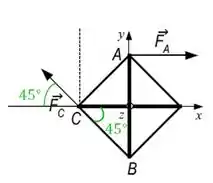
Agora é só decompor:

O enunciado fala que , então:

O exercício ainda pede pra gente calcular o torque, mas com o e é tranquilo.

Jogando tudo na relção do passo 4

c) Mesmo esquema da letra b, só que agora é em relação ao ponto A e a .

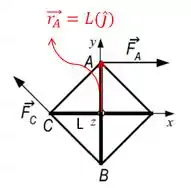
Olha que linda essa ! Não precisa ser decomposta em componentes. Lembrando que o módulo de

Então o torque vale:

Maravilha, vamos pra próxima.

d)

O torque é uma grandeza que a intensidade que faz o corpo girar. Então, como a gente já calculou o torque nas letras b e c, o corpo tá girando. Então tem uma aceleração angular, certo?

Vamo calcular ela agora! Acompanha comigo:

Ele quer a aceleração angular do objeto, então é o momento de inércia do objeto, que a gente calculou na letra a. E o torque? É o torque em todo o objeto! Ou seja, .

Beleza?

Mãos à obra

Show?

e)

Então o nosso objeto tava girando lá, aí a gente quer agora aplicar uma força horizontal no ponto B pra fazer com que o objeto pare de girar.

Primeira coisa, em que sentido o objeto tá girando?

Como que a gente descobre isso? Regra da mão direita. A aceleração angular tá em , então aponta o teu dedão pra essa direção e gira a mão. Esse é o sentido.

Sentido horário, confere?

Então se eu quiser saber uma força que faça esse giro parar, eu tenho que aplicar uma força que provoque uma rotação no sentido contrário. Olha só:

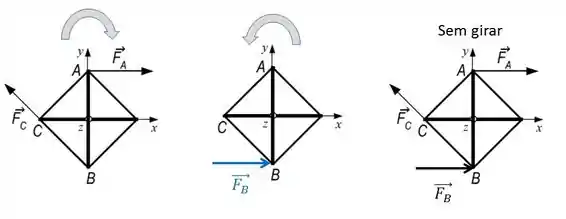
Vamos descobrir quem é essa

Se não gira, não tem torque! Então:

Opa! Apareceu a força que queremos! Como a força tá na horizontal (o enunciado fala isso), sabemos que a direção dela é .

O . Mesmo esquema que fizemos antes.

Então, cancelando os termos iguais:

Vamos escrever a forma vetorial:

Aee...vamo pra última!!

f)

Agora q gente tem que descobrir a força que o eixo de rotação faz no objeto pra que ele fique em equilíbrio estático. Isso é tranquilo! É a condição:

Só isso..viu? tranquilão

Então, vamo lá. Quem são as forças em X:

Quem são as forças em Y?

Isso aqui são os dados que a gente tem:

Agora é so substituir os dados quem está na direção X e quem está na direção Y.

Ajeitando pra uma grandeza vetorial:

Maravilha!