A haste de comprimento e massa está livre para girar em torno de um pino fixo na direção do eixo 𝑧. A haste é largada do repouso na posição horizontal e quando chega na posição vertical, sua extremidade inferior colide na altura do centro de massa de um disco de massa e raio . Ele está em repouso sobre uma superfície horizontal com coeficientes de atrito cinético e estático iguais a e respectivamente. Ao final do trajeto a superfície se inclina com um ângulo em relação à horizontal.
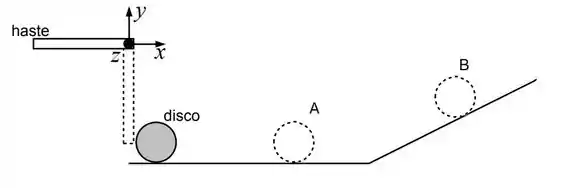
a) Quando a haste chega na posição vertical, imediatamente antes da colisão, sua velocidade na extremidade é . Imediatamente após a colisão o disco tem movimento só de translação com velocidade linear Determine a velocidade linear na extremidade da haste imediatamente após a colisão.
b) Após o deslizamento inicial, o disco passa a rolar sem deslizar ao longo da superfície horizontal com velocidade linear no centro de massa constante . Determine a energia cinética do disco.
c) Desenhe na figura acima todas as forças que agem sobre o disco enquanto ele rola sem deslizar na superfície horizontal (posição A) e enquanto ele sobe a superfície inclinada também rolando sem deslizar (posição B).
d) Determine a altura máxima que o disco alcança em relação à base da superfície inclinada. Justifique sua resposta.
Passo 1
a)
Vamos lá. Vamos pegar algumas informações importantes do enunciado:
A barra tem comprimento e massa e , respectivamente, e a velocidade inicial dela é zero.
O disco tem raio e massa , e a velocidade inicial dele é zero.
Em relação a superfície: Tem atrito! E depois de uma distância, ela é inclinada.
Outra coisa que podemos dizer: Tem coisa girando...isso quer dizer que temos momento angular! Sem pânico!! Acompanha aqui comigo.
Vamos ver o que ele tá pedindo.
Passo 2
Ele tá querendo a velocidade da barra depois da colisão.
Pensa comigo, a gente pode achar a velocidade angular também, porque se eu tiver uma, eu tenho a outra pela seguinte relação:
Onde esse R é o raio da trajetória circular.
Ah, beleza! E quem é esse raio nesse nosso problema?
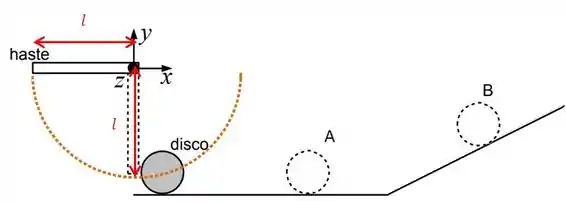
Então o raio da trajetória circular é . Aí a equação fica:
Aí, por exemplo, a velocidade angular da haste quando ela chega na posição mais baixa é:
Maravilha...Vamos continuar
Passo 3
Passo 4
A haste tá girando, né? E além disso, temos alguma força externa ao sistema haste+disco que esteja gerando torques? Não!! Por isso o momento angular do sistema é conservado!
Só uma observação importante: o momento angular se conserva em relação a um eixo! Mas calma, a gente já vai entender isso melhor.
O nosso momento angular está se conservando em relação ao eixo z:
Nessa figura que a gente vê que a conservação do momento angular é em relação ao eixo z. Então os momentos angulares têm que ser calculados em relação à ele.
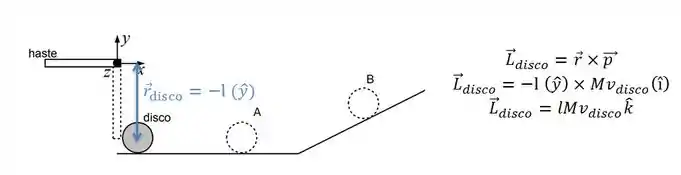
Passo 5
Pra gente resolver essa equação:
Precisamos do em relação ao eixo que tá passando pela extremidade dela. Se o valor foi dado, aí é show! Mas fica atento, porque o dado pode ser o momento de inércia da haste em relação a um eixo que passa pelo centro de massa. Se for esse o caso, também é tranquilo de resolver...a gente usa o teorema dos eixos pararelos:
A gente quer saber o . E esse D é a distância entre o CM do objeto até o eixo...Vamos lá, é moleza:
Show, vamos voltar pra equação de conservação do momento angular.
Passo 6
Substituindo os valores que o enunciado fala pra gente, o e o que a gente achou lá no passo 2:
Como a velocidade angular é zero, a velocidade linear também é!
Passo 7
b)
Agora ele quer saber a energia cinética do disco depois da colisão.
Bem, enquanto o disco gira, ele vai indo para a direita, certo? Isso quer dizer que além de girar, o cento de massa tá andando também. Por isso temos e :
O é um valor conhecido e é igual a
A velocidade angular do disco é dada pela relação do passo 2, já que temos a velocidade linear.
Então:
Show! Vamos pra próxima.
Passo 8
c)
Agora temos que fazer aquele famoso diagrama de corpo livre, que é mostrar todas as forças atuando no corpo.
Vamos lá, na posição A: Temos o peso, porque o corpo tem massa. Temos a Normal, porque o corpo está sobre uma superfície. Temos força de atrito?Opaaaa!!! Aqui mora o perigo! Vamos resolver isso agora, pra isso vamos entender o que significa rola sem deslizar.
Rolar sem deslizar só quer dizer que o ponto de contato entre a pista e o disco está em repouso, mas é só aquele pontinho lá, e é momentâneo.
Ah tá, já sei agora o que isso quer dizer....Mas, por que é importante????Porque se aquele pontinho de contato tá em repouso não há dissipação de energia mecânica pelo atrito.
O que acontece é que como a velocidade ali naquele ponto é zero, e olha lá, ele falou na letra b que aquele é constante, certo? Então a aceleração é nula, logo a força resultante em é nula…
A, na posição A, tá em portanto ela é nula!!!!
Agora vamos ver na posição B.
O peso tá pra baixo e a normal é perpendicular a superfície. Continuamos com a condição de que a velocidade no ponto B seja nula, pra velocidade ali ser nula, a força resultante tem que ser zero! Então decompondo o peso, colocamos a, contra a tendência de movimento, de forma a anular a componente do peso. Olha só:
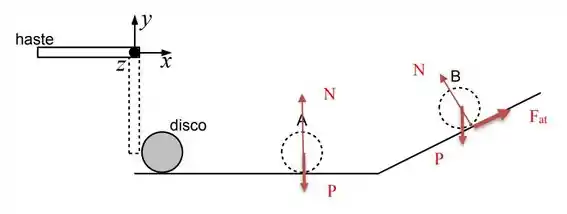
Passo 9
Show??
Passo 10
d)
Agora ele quer o quanto o disco conseguiu subir o plano inclinado.
Lembra que a gente falou lá na letra c que o rolamento sem deslizamento conserva energia mecânica. Então vamos fazer a conservação desde o momento em que o disco começa a girar, e está lá no plano. Até que ele para quando atinge a altura máxima.
Suave??
Resposta
a)
b)
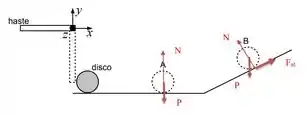 c)
c)
d)