P3 de Física B - FIS1026 da PUCRIO - 2019.1

Parte 1 – Uma roda de bicicleta é constituída por um aro de raio e por barras que sustentam o aro em torno de um eixo de rotação conforme a figura. A massa do aro vale e de cada uma das barras vale . Determine o momento de inércia desta roda. (O momento de inércia de uma barra girando em torno de seu centro de massa ale ).

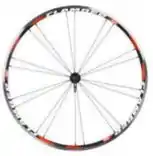
Parte 2 – Uma roda com momento de inércia se encontra girando a uma velocidade angular de . Esta roda é então freada com uma aceleração angular constante de até parar.

a) Determine a energia cinética inicial da roda.

b) Determine o tempo necessário e o ângulo percorrido em radianos até a roda parar.

Parte 3 – Um disco gira no plano com aceleração angular dada por , onde é o tempo.

a) Se o disco possui velocidade angular inicial , escreva a equação para a velocidade angular.

b) Determine o vetor velocidade angular do disco no instante onde .

Um engenheiro monta um sistema que se constitui de dois cilindros de raios e unidos de forma que o centro da face circular do primeiro cilindro coincida com o centro da face circular do segundo. Em cada um dos cilindros com diferentes raios é enrolado um fio ideal. Este sistema pode girar sem atrito em torno de um eixo colocado no centro da face circular dos cilindros. O sistema pode ser observado nas figuras abaixo com visão lateral e frontal. A massa do cilindro menor de raio vale e a massa do cilindro de maior raio vale . O raio é igual ao dobro de . Para a aceleração da gravidade adote .

O momento de inércia de um disco girando em torno do seu centro de massa vale .

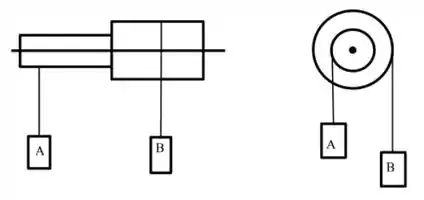
a) Escreva o momento de inércia deste sistema envolvendo os dois cilindros girando em torno do eixo apresentado na figura em termos de suas massas e dos seus raios.

b) Duas massas e são colocadas nos fios enrolados em cada um dos cilindros conforme a figura do enunciado. Faço o diagrama de corpo livre representando as forças que atuam na massa A, na massa B e no cilindro.

c) Em termos dos dados apresentados, escreva qual deve ser a relação entre as massas e para o sistema ficar em repouso em função das variáveis do problema dadas no enunciado.

d) Suponha que seja igual a e lembrando que . Nesta condição o sistema entrará em movimento. Calcule a aceleração angular dos cilindros em termos das variáveis dadas no enunciado.

e) Na condição dada no item (d), com e , sabe-se que o sistema se encontra inicialmente em repouso. Após o sistema ser liberado ele entra em movimento. Determine a velocidade angular dos cilindros após a massa A se deslocar de uma altura (a massa B irá se deslocar de ) em termos das variáveis dadas no enunciado utilizando a conservação de energia mecânica.

Um corpo uniforme de massa está preso a um fio ideal de massa desprezível que passa por um buraco no centro da superfície. A superfície se encontra no plano . O corpo está inicialmente descrevendo uma trajetória circular em sentido anti-horário sobre a superfície horizontal com velocidade linear inicial e raio inicial medido a partir do seu centro de massa de . O fio é puxado por uma força após o fio ter passado pelo buraco conforme a figura.

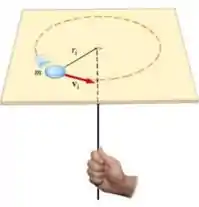
Quando a força para de atuar, o raio da trajetória final é de . Desconsidere o atrito entre o fio e o buraco e entre o corpo e a superfície.

a) Determine o vetor momento angular inicial do corpo girando em torno do eixo de rotação.

b) Determine o vetor velocidade angular final do corpo.

c) Encontre o trabalho realizado pela força sobre o corpo.

d) Marque a única alternativa correta: Após ter reduzido o raio da trajetória em relação a trajetória inicial,

(i) o momento angular e a energia cinética se conservam pois não há força externa atuando no sistema.

(ii) o momento angular se conserva pois não há forças externas produzindo um torque no sistema e a energia cinética não se conserva.

(iii) o momento angular não se conserva, pois a força produz um torque externo no sistema e a

energia cinética se conserva pois não há colisão.

(iv) o momento angular não se conserva, pois a força produz um torque externo no sistema e a

energia cinética não se conserva.

(v) o momento de inércia do sistema muda, por isso não se conservam nem o momento angular e nem a energia cinética.

(vi) Nenhuma das afirmações anteriores está correta.