Um corpo uniforme de massa está preso a um fio ideal de massa desprezível que passa por um buraco no centro da superfície. A superfície se encontra no plano . O corpo está inicialmente descrevendo uma trajetória circular em sentido anti-horário sobre a superfície horizontal com velocidade linear inicial e raio inicial medido a partir do seu centro de massa de . O fio é puxado por uma força após o fio ter passado pelo buraco conforme a figura.
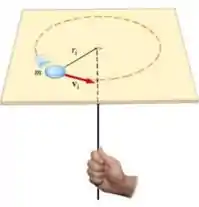
Quando a força para de atuar, o raio da trajetória final é de . Desconsidere o atrito entre o fio e o buraco e entre o corpo e a superfície.
a) Determine o vetor momento angular inicial do corpo girando em torno do eixo de rotação.
b) Determine o vetor velocidade angular final do corpo.
c) Encontre o trabalho realizado pela força sobre o corpo.
d) Marque a única alternativa correta: Após ter reduzido o raio da trajetória em relação a trajetória inicial,
(i) o momento angular e a energia cinética se conservam pois não há força externa atuando no sistema.
(ii) o momento angular se conserva pois não há forças externas produzindo um torque no sistema e a energia cinética não se conserva.
(iii) o momento angular não se conserva, pois a força produz um torque externo no sistema e a
energia cinética se conserva pois não há colisão.
(iv) o momento angular não se conserva, pois a força produz um torque externo no sistema e a
energia cinética não se conserva.
(v) o momento de inércia do sistema muda, por isso não se conservam nem o momento angular e nem a energia cinética.
(vi) Nenhuma das afirmações anteriores está correta.
Passo 1
Fala pessoal, bora resolver esse problema sobre conservação do momento angular?
O momento angular de uma partícula é definido por
Para uma partícula em movimento circular, temos
Substituindo os valores:
O vetor deve apontar na direção , de modo que o vetor momento angular inicial é
Passo 2
Para resolver o item (b) vamos usar a conservação do momento angular:
Como , temos que
Substituindo os valores:
Assim, o vetor velocidade angular é
Passo 3
No item (c) queremos achar o trabalho da força . Basta lembrar que o trabalho é igual a variação da energia cinética:
Já sabemos que , enquanto
Portanto,
Passo 4
No último item temos que ver qual afirmação é verdadeira. Como a única força externa sobre o sistema atua sobre o eixo, o torque sobre o sistema é nulo. Com isso, o momento angular do sistema se conserva (usamos isso no item (b)).
Por outro lado, vimos no item (c) que a energia cinética não se conserva, já que um trabalho externo é feito sobre o sistema. Portanto, a afirmativa correta é a (ii)!