Um engenheiro monta um sistema que se constitui de dois cilindros de raios e unidos de forma que o centro da face circular do primeiro cilindro coincida com o centro da face circular do segundo. Em cada um dos cilindros com diferentes raios é enrolado um fio ideal. Este sistema pode girar sem atrito em torno de um eixo colocado no centro da face circular dos cilindros. O sistema pode ser observado nas figuras abaixo com visão lateral e frontal. A massa do cilindro menor de raio vale e a massa do cilindro de maior raio vale . O raio é igual ao dobro de . Para a aceleração da gravidade adote .

O momento de inércia de um disco girando em torno do seu centro de massa vale .

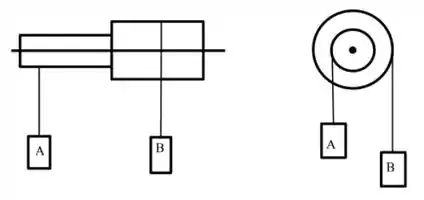
a) Escreva o momento de inércia deste sistema envolvendo os dois cilindros girando em torno do eixo apresentado na figura em termos de suas massas e dos seus raios.

b) Duas massas e são colocadas nos fios enrolados em cada um dos cilindros conforme a figura do enunciado. Faço o diagrama de corpo livre representando as forças que atuam na massa A, na massa B e no cilindro.

c) Em termos dos dados apresentados, escreva qual deve ser a relação entre as massas e para o sistema ficar em repouso em função das variáveis do problema dadas no enunciado.

d) Suponha que seja igual a e lembrando que . Nesta condição o sistema entrará em movimento. Calcule a aceleração angular dos cilindros em termos das variáveis dadas no enunciado.

e) Na condição dada no item (d), com e , sabe-se que o sistema se encontra inicialmente em repouso. Após o sistema ser liberado ele entra em movimento. Determine a velocidade angular dos cilindros após a massa A se deslocar de uma altura (a massa B irá se deslocar de ) em termos das variáveis dadas no enunciado utilizando a conservação de energia mecânica.

No item (b) ele pede para desenharmos as forças sobre cada corpo:

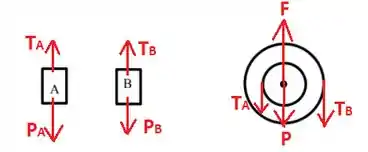
Nos blocos A e B as forças serão peso e tração. Nos cilindros teremos a tração, o peso dos cilindros e uma força de sustentação aplicada pelo eixo sobre os cilindros, mas que não afeta em nada a rotação do sistema.

No item (c) nós queremos achar uma relação entre as massas dos blocos para que o sistema fique em repouso. Para que isso ocorra, o torque resultante sobre os cilindros deve ser nulo!

Adotando o sentido positivo de rotação como sendo o horário, o torque é dado por

Além disso, podemos escrever a segunda lei de Newton para cada bloco. Como adotamos o sentido positivo como sendo o horário, para o bloco B a aceleração positiva indica que ele desce, enquanto para o bloco A indica que ele sobe:

Com isso, temos que

Da condição que o sistema fica em repouso, temos e , de modo que

Assim,

Logo,

Agora vamos para o item (d), em que devemos considerar . Queremos achar a aceleração angular do sistema. Para isso, usamos a segunda lei de Newton para a rotação:

Assim, usando o resultado do passo anterior:

Além disso, temos o sistema

Daí, temos que

Só falta relacionar e com :

Portanto,

Logo,

Vou deixar a resposta em função de para não ficar uma coisa muito feia. Lembre-se que achamos no item (a).

Para terminar o problema falta só fazer o item (e)! Estamos na mesma condição do item (d) com . Vimos que a aceleração angular é positiva, de modo que nessa condição o sistema gira no sentido horário, o bloco B cai uma altura e o bloco A sobe uma altura .

Nós queremos saber qual é a velocidade angular do sistema após o bloco A subir uma altura e o bloco B descer , considerando que inicialmente o sistema estava todo parado.

Para isso, vamos calcular o trabalho do peso no bloco A e no bloco B:

Observe que o trabalho sobre o bloco A é negativo pois ele sobe contra o peso. Com isso, o trabalho resultante é

Esse trabalho será igual a variação de energia cinética do sistema:

Como inicialmente o sistema está em repouso, temos :

A energia cinética terá três parcelas:

O grande passo é perceber que

Assim,

Portanto,

E desta forma nós fechamos o problema 😉!