Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 421234567891011121314151617181920212223242526272829303132333435363738394041434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

Física B – PUC RJ – 2019.1 – P3 – Questão 1

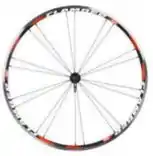
Parte 1 – Uma roda de bicicleta é constituída por um aro de raio r = 25   c m e por 20 barras que sustentam o aro em torno de um eixo de rotação conforme a figura. A massa do aro vale 100   g e de cada uma das barras vale 10   g . Determine o momento de inércia desta roda. (O momento de inércia de uma barra girando em torno de seu centro de massa ale I C M - b a r r a = M L 2 / 12 ).

Parte 2 – Uma roda com momento de inércia I = 2 ⋅ 10 - 3   k g   m 2 se encontra girando a uma velocidade angular de 80   r a d / s . Esta roda é então freada com uma aceleração angular constante de - 2   r a d / s 2 até parar.

a) Determine a energia cinética inicial da roda.

b) Determine o tempo necessário e o ângulo percorrido em radianos até a roda parar.

Parte 3 – Um disco gira no plano x y com aceleração angular dada por α = t 2 + 3 t r a d / s 2 , onde t é o tempo.

a) Se o disco possui velocidade angular inicial ω 0 , escreva a equação para a velocidade angular.

b) Determine o vetor velocidade angular do disco no instante t = 3   s onde ω 0 = 2   r a d / s .

Passo 1

Fala galerinha, beleza?

Na parte 1 desse problema ele quer que calculemos o momento de inércia da roda, composta pelo aro e por 20 barras. Observe pelo desenho que, ao invés de trabalharmos com 20 barras de comprimento r = 25   c m , nós podemos trabalhar com 10 barras de comprimento L = 2 r = 50   c m e massa m = 20   g com eixo de rotação no centro de massa. O momento de inércia de uma dessas barras é

I b a r r a = m L 2 12

Considerando todas as barras:

I t o d a s b a r r a s = 10 m L 2 12 = 5 m r L 2 6

Já para o aro, como toda massa está a uma distância r do eixo de rotação, o momento de inércia é simplesmente

I a r o = M r 2

Assim, o momento de inércia total é a soma dos dois:

I = M r 2 + 5 m L 2 6

Daí é só fazer conta:

I = 0,1   k g ⋅ 0,25 2   m 2 + 5 6 ⋅ 0,02   k g ⋅ 0,5 2   m 2

I = 0,00625   k g   m 2 + 0,00417   k g   m 2

Assim,

I = 0,01042   k g   m 2

Passo 2

Na parte 2 temos uma nova roda, com I = 2 ⋅ 10 - 3   k g   m 2 . No item (a) queremos a energia cinética inicial da roda, dada por

K i = I ω i 2 2 = 2 ⋅ 10 - 3 ⋅ 80 2 2

Logo,

K i = 6,4   J

No item (b) ele quer saber o tempo que demorar para a roda parar e o ângulo percorrido. Podemos usar as expressões do MUV adaptadas ao variáveis angulares:

ω = ω 0 + α t

ω 2 = ω 0 2 + 2 α θ

Só podemos usar essas expressões pois a aceleração angular é constante! Substituindo ω = 0 :

0 = 80 - 2 t → t = 40   s

0 = 80 2 - 2 ⋅ 2 ⋅ θ → θ = 1600   r a d

Passo 3

Por fim, vamos a parte 3! Agora a aceleração angular não é mais constante:

α t = t 2 + 3 t

Como

α = d ω d t ,

temos que

ω = ω 0 + ∫ α   d t

Assim,

ω = ω 0 + ∫ t 2 + 3 t   d t

Portanto,

ω t = ω 0 + t 3 3 + 3 t 2 2

Passo 4

Usando ω 0 = 2   r a d / s , no instante t = 3   s temos

ω 3 = 2 + 27 3 + 27 2 = 24,5   r a d / s

Como o disco gira no plano x y e o vetor velocidade angular deve ser perpendicular a esse plano, temos que

ω → = 24,5   z ^   r a d / s

E assim fechamos o problema 😊!

Resposta

I = 0,01042   k g   m 2

K i = 6,4   J

t = 40   s ,             θ = 1600   r a d

ω t = ω 0 + t 3 3 + 3 t 2 2

ω → = 24,5   z ^   r a d / s

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que