P3 de Física B - FIS1026 da PUCRIO - 2019.2

Uma corda ideal está enrolada na periferia de uma casca esférica (massa e raio ) que gira em torno de um eixo vertical. A corda conecta a casca a uma roldana ( e ) e finalmente a um bloco pendurado de massa . A corda não desliza sobre a casca nem sobre a roldana e a casca e a roldana giram sem atrito em torno de seus eixos. Considere , e .

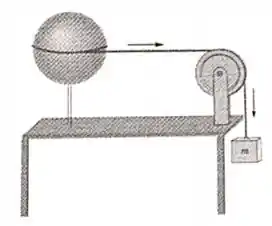
Com o sistema partindo do repouso, o bloco desce com aceleração e a roldana sofre deslocamento angular até que o bloco esteja na iminência de tocar o solo.

a) Calcule o tempo de queda do bloco e a velocidade angular final da casca.

b) Para o bloco, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.

c) Para a casca, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.

d) Para a roldana, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.

e) Determine o valor da massa do bloco.

Dois fios ideais estão enrolados na periferia de um cilindro de comprimento , raio e massa . O cilindro é abandonado a partir do repouso e passa a cair na vertical sem escorregar nos fios. Considere e .

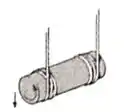
Para o instante em que o eixo do cilindro tiver descido a distância vertical de , calcule:

a) a energia cinética de translação do cilindro;

b) a energia cinética de rotação do cilindro.

Considere agora um segundo cilindro de mesmo , mesmo e mesma massa que o anterior, mas com massa distribuída de modo diferente de tal modo que , onde é um fator adimensional menor ou igual a .

c) Calcule o valor de sabendo que, após cair a partir do repouso, a velocidade escalar de seu centro de massa vale .

Uma esfera maciça homogênea, de massa e raio , está fixada por sua periferia à extremidade de uma barra fina homogênea, de massa e comprimento . O conjunto barra-esfera está disposta sobre uma mesa horizontal sem atrito, de modo que pode girar livremente em torno de . Considere as seguintes expressões para os momentos de inércia em torno dos centros de massa: e .

a) Calcule, em , o momento de inércia do conjunto barra-esfera em relação ao ponto .

O conjunto barra-esfera, inicialmente em repouso, recebe o impacto de uma bala de massa que se dirige perpendicularmente à barra com velocidade escalar . Como resultado deste impacto de duração muito curta, a bala acaba se alojando exatamente no centro da esfera, e o novo conjunto, barra-esfera-bala, passa a rodar em torno de .

b) Julgue cada afirmativa como Verdadeira ou Falsa e depois justifique sua resposta.

(i) A energia cinética total do sistema barra-esfera-bala é conservada durante a colisão.

(ii) O momento linear total do sistema barra-esfera-bala é conservado durante a colisão.

(iii) O momento angular total do sistema barra-esfera-bala é conservado durante a colisão.

Considere a massa da bala e suponha que o valor encontrado no item (a) para o momento de inércia do conjunto barra-esfera tenha sido .

c) Calcule a velocidade escalar que a bala possuía imediatamente antes do impacto sabendo que, imediatamente após o impacto, o sistema barra-esfera-bala gira ao redor de com velocidade angular final .