Uma corda ideal está enrolada na periferia de uma casca esférica (massa e raio ) que gira em torno de um eixo vertical. A corda conecta a casca a uma roldana ( e ) e finalmente a um bloco pendurado de massa . A corda não desliza sobre a casca nem sobre a roldana e a casca e a roldana giram sem atrito em torno de seus eixos. Considere , e .
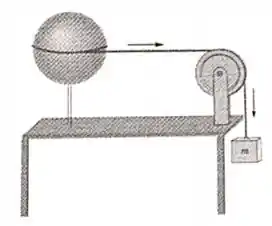
Com o sistema partindo do repouso, o bloco desce com aceleração e a roldana sofre deslocamento angular até que o bloco esteja na iminência de tocar o solo.
a) Calcule o tempo de queda do bloco e a velocidade angular final da casca.
b) Para o bloco, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
c) Para a casca, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
d) Para a roldana, represente num diagrama de forças as forças relevantes para seu movimento de translação e escreva a Segunda Lei de Newton associada.
e) Determine o valor da massa do bloco.
Passo 1
Fala galerinha, bora resolver mais uma questão?
Sabemos qual é aceleração do bloco e, consequentemente, do fio. Para achar a aceleração angular da roldana e da casca, usamos
Assim,
Como a aceleração é constante, podemos usar a expressão:
Como , temos que
Para achar a velocidade angular da casca
Passo 2
No item (b) vamos olhar para o bloco:
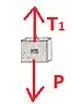
Nesse caso, a segunda lei de Newton para translação é escrita como
Ou ainda,
Passo 3
No item (c) temos que fazer o mesmo para a casca:

Assim, a segunda lei de Newton da rotação fica
Passo 4
Por fim, no item (d) olhamos para a roldana:
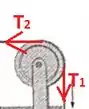
Assim,
Passo 5
Já sabemos que , e . Vamos calcular os momentos de inércia:
Do passo 3, temos que
Já do passo 4,
Assim, usando o resultado do passo 2:
E assim terminamos mais um problema!