Física B – PUC RJ – 2019.2 – P3 – Questão 2
Dois fios ideais estão enrolados na periferia de um cilindro de comprimento , raio e massa . O cilindro é abandonado a partir do repouso e passa a cair na vertical sem escorregar nos fios. Considere e .
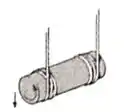
Para o instante em que o eixo do cilindro tiver descido a distância vertical de , calcule:
a) a energia cinética de translação do cilindro;
b) a energia cinética de rotação do cilindro.
Considere agora um segundo cilindro de mesmo , mesmo e mesma massa que o anterior, mas com massa distribuída de modo diferente de tal modo que , onde é um fator adimensional menor ou igual a .
c) Calcule o valor de sabendo que, após cair a partir do repouso, a velocidade escalar de seu centro de massa vale .
Passo 1
Fala pessoal, prontos para mais uma questão?
Os dois primeiros itens a gente resolve junto: basta usar a conservação da energia!
Inicialmente a energia mecânica era toda potencial gravitacional. Com a queda, essa energia potencial se converte em energia cinética, uma parcela de translação e outra de rotação:
Daí usamos
Assim,
Logo,
Passo 2
A energia de translação é dada por
Já a de rotação é
Passo 3
Para o item (c) o momento de inércia agora é . Assim, a conservação de energia nos fornece
Portanto,
Simplificando as massas:
Portanto,
Ou ainda,
Com isso finalizamos mais um problema 😉.