P1 de Mecânica 1 da USP - 2021.2

1) Considere o movimento plano da barra AB mostrado no desenho, de comprimento , e articulada sem atrito pelas suas extremidades aos centros de dois discos idênticos de raio R. Os discos mantêm contato com a respectiva superfície e rolam sem escorregar, de modo que o ponto B percorre o eixo e o ponto A percorre o eixo . O referencial fixo é o solo e sabe-se que o vetor de rotação da barra AB é com constante. A partir do instante inicial , quando temos . O sistema de coordenadas é fixo.

São dados: , , .

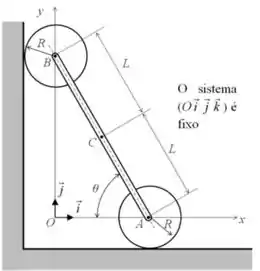
Para os itens (a) até (e) considere o sistema no instante inicial, quando a barra AB está na vertical .

a) Usando a propriedade fundamental da cinemática do corpo rígido, calcule a velocidade do ponto B.

b) Localize o centro instantâneo de rotação (CIR) do disco de centro A.

c) Localize o CIR da barra AB.

d) Determine o vetor de rotação do disco de centro A.

e) Calcule a aceleração do ponto B da barra AB.

f) No instante em que a barra AB está a , calcule a velocidade do centro C da barra AB, expressando-a no sistema de coordenadas intrínseco.

2) A figura mostra uma barra homogênea de comprimento e massa apoiada sobre um disco de massa e raio que se encontra apoiado no plano inclinado de um ângulo em relação à horizontal; o vínculo em A é uma articulação, o plano inclinado é fixo e o sistema está em equilíbrio estático. O coeficiente de atrito é o mesmo nos pontos de contato B e C, os vetores devem ser expressos no sistema de coordenadas de eixos de versores , respectivamente, indicado na figura.

São dados: kg, kg, , .

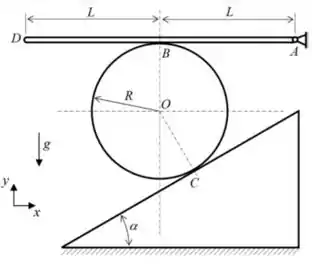
Determine:

a) A reação vincular no ponto A da barra.

b) A força de atrito aplicada no disco pela barra no ponto B.

c) A força normal aplicada no disco pela barra no ponto B.

d) A força de atrito aplicada no disco pelo plano inclinado no ponto C.

e) O valor mínimo do coeficiente de atrito para que não ocorra escorregamento no contato em B.