PSUB de Mecânica 1 da USP - 2018

01) Um Corpo rígido de massa é formado por duas barras, e , soldadas perpendicularmente em (ponto médio de ), conforme ilustrado na figura. Estas barras são homogêneas, esbeltas e tem comprimento cada. A extremidade do corpo rígido encontra-se articulada a um bloco que desliza sobre uma guia horizontal com uma aceleração , conhecida. Pede-se:

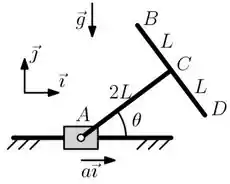
a) O vetor posição do centro de massa do corpo rígido formado pelas barras e .

b) O momento de inércia , do corpo rígido com respeito ao eixo .

c) O diagrama de corpo livre do corpo rígido.

d) O valor do ângulo para o qual a aceleração angular do corpo rígido é nula.

Dado: o momento de inércia de uma barra homogênea e esbelta de massa e comprimento com respeito a um eixo perpendicular passante por seu centro de massa é igual a .

02) Considere o sistema ilustrado na figura, em que os discos e , de centros e , respectivamente, são vinculados entre si por meio de uma articulação ideal localizada na periferia de ambos, em . Há ainda, em , uma articulação que vincula o disco a uma base fixa com respeito a um referencial inercial. Denote por e as respectivas acelerações angulares dos discos e . Admita que os discos são idênticos, homogêneos e têm massa e raio . Para a configuração indicada na figura, em que as linhas e estão na vertical e horizontal, respectivamente, e admitindo que os discos encontram-se inicialmente em repouso, pede-se, para o instante imediatamente após a liberação do sistema:

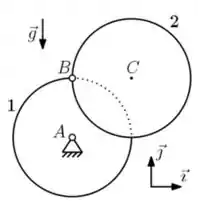
a) Os diagramas de corpo livre para cada um dos discos.

b) As expressões das acelerações dos pontos e em função de e .

c) Os valores de e .

d) A força aplicada pelo disco de centro sobre o disco de centro por meio da articulação em .

Dado: para o disco de centro ,

03) Um disco homogêneo, de massa e raio , pode rolar sem escorregar sobre uma superfície plana horizontal que está fixa com respeito a um referencial inercial. A mola linear, de rigidez e comprimento natural , está vinculada a uma base fixa em e ao disco em seu centro . Seja o ângulo entre e a vertical , indicado na figura. Pede-se:

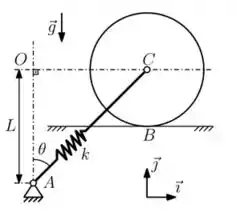
a) O diagrama de corpo livre para o disco.

b) As expressões, em termos de e , do vetor posição , da velocidade do ponto e da velocidade angular do disco.

c) A expressão da energia cinética do sistema.

d) A expressão da energia potencial do sistema.

e) Considerando que o sistema parta do repouso na configuração , determine o vetor de rotação do disco quando o sistema atingir pela primeira vez a configuração .

Dado: para o disco,