1) Considere o movimento plano da barra AB mostrado no desenho, de comprimento , e articulada sem atrito pelas suas extremidades aos centros de dois discos idênticos de raio R. Os discos mantêm contato com a respectiva superfície e rolam sem escorregar, de modo que o ponto B percorre o eixo e o ponto A percorre o eixo . O referencial fixo é o solo e sabe-se que o vetor de rotação da barra AB é com constante. A partir do instante inicial , quando temos . O sistema de coordenadas é fixo.

São dados: , , .

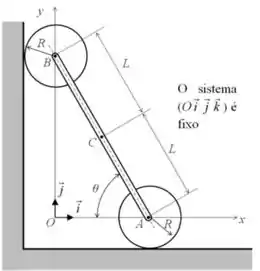
Para os itens (a) até (e) considere o sistema no instante inicial, quando a barra AB está na vertical .

a) Usando a propriedade fundamental da cinemática do corpo rígido, calcule a velocidade do ponto B.

b) Localize o centro instantâneo de rotação (CIR) do disco de centro A.

c) Localize o CIR da barra AB.

d) Determine o vetor de rotação do disco de centro A.

e) Calcule a aceleração do ponto B da barra AB.

f) No instante em que a barra AB está a , calcule a velocidade do centro C da barra AB, expressando-a no sistema de coordenadas intrínseco.

b) Precisamos determinar a posição do centro instantâneo (CIR) de rotação do disco centrado em A.

Tem uma dica muito boa para determinarmos onde está o CIR:

- Escolhemos dois pontos do nosso corpo que sabemos o sentido das suas velocidades.- Traçamos duas retas perpendiculares às suas velocidades, passando pelos próprios pontos.

Onde ocorrer a intersecção, trata-se de um CIR. É por isso que pontos com velocidade nula são um CIR logo de cara.

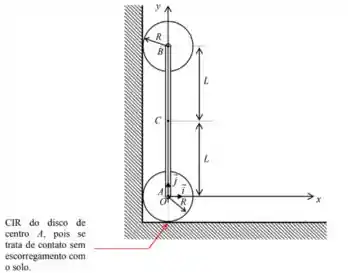
No lugar da reta que traçaríamos perpendicular a velocidade desse ponto, como , temos apenas o próprio ponto. De modo que ele, obrigatoriamente é um CIR.

Sendo assim, como é falado no enunciado que o disco A rola sem escorregar, o ponto de contato do disco com o solo será um CIR, como indica a figura acima.

Portanto:

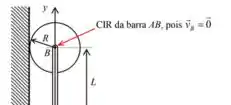
c) Devemos determinar o CIR da barra AB. Porém, já encontramos no item A que . Logo, B é um centro instantâneo de rotação para a barra AB. Portanto:

d) Agora precisamos calcular o vetor de rotação do disco centrado em A.

A ideia aqui é primeiro calcularmos a velocidade de A em função de . Daí, usando o fato de B ser um CIR para os pontos da barra (incluindo A), vem que:

Agora, sabendo que o vetor de rotação deverá obedecer a:

Igualando os dois resultados, chegamos que:

Logo:

Substituindo os dados da questão:

Excelente! Já podemos ir para a próxima.

e) Nesse item devemos calcular a aceleração de B. À primeira vista pode parecer bem complicado, porque costumamos calcular acelerações identificando um ponto que já sabemos o valor de e usando a ideia de aceleração relativa.

Mas nessa questão, não temos nenhum ponto que logo de cara já sabemos quanto vale a sua aceleração. Lembra que até agora tudo que fizemos foi para .

Uma boa opção nesses casos é voltar para a definição mais pura.

Onde é o vetor posição de B em um instante qualquer.

Em um instante qualquer, a barra estará inclinada de um ângulo . O disco B, percorre sempre o eixo , logo podemos escrever que:

Derivando essa equação a primeira vez, temos:

Derivando mais uma vez, temos:

Massa! Como a derivada do ângulo é a velocidade angular ficamos com:

Substituindo os dados:

Prontinho, essa é a resposta 😉

f) Bom, precisamos determinar no sistema de coordenadas intrínseco.

Mas vamos por partes, primeiramente bora determinar e depois nos preocupamos com esse sistema intrínseco.

Para calcular podemos usar a ideia do CIR. Seguido o procedimento mostrado no passo 2, somos capazes de encontrar a nova posição do CIR.

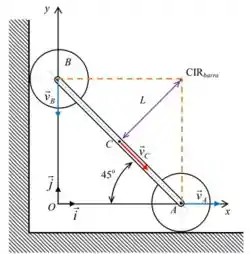
Beleza! Agora que encontramos o podemos usar que:

O Sistema de coordenadas intrínseco é um sistema que usa a direção e sentido da velocidade para determinar um versor tangente.

Assim, teremos que:

Logo:

Substituindo os dados:

Aeeee, finalmente terminamos a questão!! Todo mundo entendeu direitinho?! Até a próxima gente!!