P2 de Mecânica 1 da USP - 2020.2

1) O mecanismo ilustrado na figura abaixo é constituído por 3 componentes: 1) um suporte ABOD (desenhado em azul) vinculado à articulação A e ao mancal radial B, que gira com velocidade angular constante em torno do eixo vertical; 2) uma luva C (desenhada em verde), que desliza ao longo da haste OD do suporte ABOD com velocidade constante relativa à haste; 3) um disco de raio R, solidário à luva C que gira em torno da haste OD com velocidade angular constante . O sistema de referência móvel é ligado ao suporte ABOD e, no instante mostrado na figura, o ponto P da periferia do disco encontra-se na posição . Nota: Todas as respostas devem ser expressas no sistema de coordenadas .

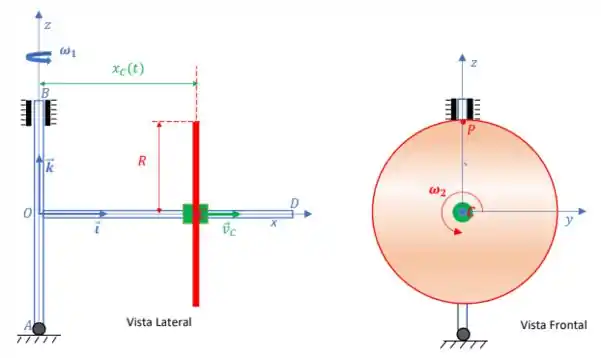
Pedem-se:

a) A velocidade absoluta do ponto C.

b) A aceleração absoluta do ponto C;

c) O vetor rotação absoluta do disco;

d) O vetor aceleração rotacional absoluta do disco;

e) A velocidade absoluta do ponto P;

f) A aceleração absoluta do ponto P.

2) Uma barra delgada e homogênea, de comprimento e massa é articulada em a uma distância do seu centro de massa, estando restrita a mover-se no plano , conforme ilustrado na figura.

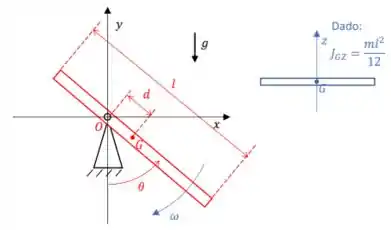
a) Determine o momento de inércia da barra.

b) Sabendo que a barra parte da posição angular com velocidade angular inicial no sentido horário, determine o menor valor de em módulo, para que a barra não mude o sentido de rotação

3) A figura abaixo representa um dispositivo robótico movendo-se num plano vertical, com aceleração da gravidade . Na extremidade A da coluna fixa há um pequeno motor elétrico que aplica um momento (anti-horário) na extremidade A do braço AB, fazendo este braço girar em torno de A com velocidade angular e aceleração angular , dados. Na extremidade B do braço AB há outro pequeno motor, que aplicar o momento (anti-horário) no braço BC, fazendo-o girar com velocidade angular e aceleração angular A massa do braço AB é , a do braço BC é e ambos podem ser considerados como hastes delgadas homogêneas.

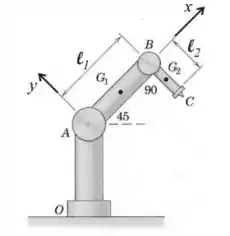
Para a posição indicada na figura, e usando o sistema de eixos indicados, pede-se:

a) Desenhar os diagramas de corpo livre dos braços AB e BC;

b) Escrever as equações do teorema da resultante (TR) e do Teorema da quantidade de movimento angular (TQMA) para o braço BC;

Supondo que o motor em B trave a conexão dos braços AB e BC na posição relativa mostrada, pede-se:

c) obter as expressões de e em função de , das massas e das dimensões dadas na figura;

d) Determinar o momento exercido pelo braço AB sobre o braço BC.