2) A figura mostra uma barra homogênea de comprimento e massa apoiada sobre um disco de massa e raio que se encontra apoiado no plano inclinado de um ângulo em relação à horizontal; o vínculo em A é uma articulação, o plano inclinado é fixo e o sistema está em equilíbrio estático. O coeficiente de atrito é o mesmo nos pontos de contato B e C, os vetores devem ser expressos no sistema de coordenadas de eixos de versores , respectivamente, indicado na figura.
São dados: kg, kg, , .
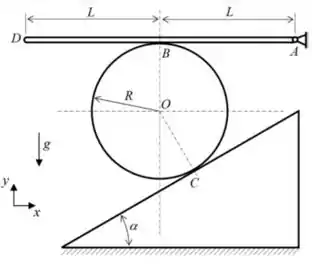
Determine:
a) A reação vincular no ponto A da barra.
b) A força de atrito aplicada no disco pela barra no ponto B.
c) A força normal aplicada no disco pela barra no ponto B.
d) A força de atrito aplicada no disco pelo plano inclinado no ponto C.
e) O valor mínimo do coeficiente de atrito para que não ocorra escorregamento no contato em B.
Passo 1
Eaíiiii gente!! Tudo certinho com vocês?
Mais uma questão de mecânica, agora misturando disco, atrito, plano inclinado e tudo o que tem direito!
a) Para começar, esse item nos pede para calcular o valor da reação vincular no ponto A da barra. Essa reação vincular nada mais é do que a reação do apoio em A, pois como a barra está articulada nesse ponto, deve haver uma reação vertical e horizontal ali.
Uma boa forma de conseguir identificar as equações de equilíbrio é desenharmos o diagrama de corpo livre (DCL) da nossa barra AD.
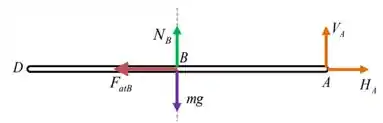
Beleza! Podemos agora escrever as equações de equilíbrio tanto de força como de momento:
Usando (3) em (2), vamos ficar com:.
Beleza, já matamos uma parte da reação vincular em A. Mas ainda precisamos calcular para conseguir determinar .
Como já usamos nossas 3 equações do equilíbrio, vamos tentar encontrar essa força analisando o DCL do disco.
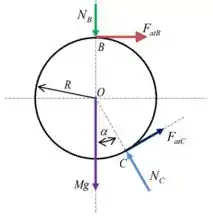
Lembrando que , escrevendo as equações de equilíbrio de momento, ficamos com:
Em relação a :
Em relação a , vamos ter:
Olha só, excelente! Conseguimos descobrir , logo usando a nossa equação (1) lá do início, vamos ter:
Agora colocando só na forma de vetor, e levando em conta também que , temos:
Como kg, kg, , , ficamos com:
Prontinho! Foi um pouco longa, mas os resultados que encontramos aqui vão nos ajudar no restante da questão 😊
Passo 2
b) Agora ele nos pede para determinar a força de atrito que atua no ponto B, ou seja, o atrito entre o disco e a barra. Mas, como eu falei pra vocês, no item A encontramos muitos resultados que vão ser úteis.
Lá na equação (5) encontramos que:
Esse resultado é em módulo, mas pelo DCL sabemos também a direção e sentido dessa força. Aqui é importante ter cuidado com a interpretação do enunciado, pois ele pede a força de atrito aplica no disco, então temos que considerar o apontando para .
Logo:
Como kg, kg, , , ficamos com:
Passo 3
c)
Nesse item nos é pedido a força normal aplicada no ponto B do disco pela barra, ou seja, .
No item a já calculamos a intensidade desse vetor, pelo DCL do disco vemos também que essa força aponta para o sentido .
Logo, podemos escrever que:
Como kg e :
Passo 4
d)
Olha aí, nada novo debaixo do sol. Mais uma vez é pedido algo que já calculamos na letra a, uhuuul!Devemos encontrar o a força de atrito aplicada no ponto C do disco, pelo plano inclinado.
Pela equação (4) do item a, temos que:
Mas, já sabemos o valor de . Daí:
Para determinar as componentes em e , vamos analisar a geometria da figura abaixo:
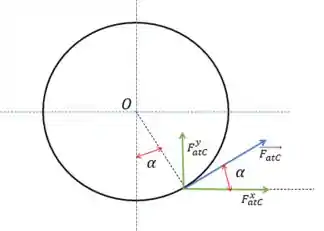
Daí, temos que:
Logo, juntando os dois podemos escrever que:
Como kg, kg, , , ficamos com:
Passo 5
e)
Aee, última letra da questão!
Pra finalizar, precisamos determinar o valor mínimo do coeficiente de atrito de modo que não ocorra escorregamento em B, ou seja, o equilíbrio estático seja mantido naquele ponto.
Esse tipo de pergunta é bem comum em questões envolvendo atrito na mecânica. O importante pra entender bem ela, é refinar um pouco o nosso conceito da força de atrito.
A ideia é que a força de atrito é sempre menor ou igual que o produto pela normal no ponto de contato. Muitas vezes confundimos esse conceito e consideramos a igualdade logo de cara, mas ela nem sempre é válida. Portanto, temos que:
Logo, o menor valor possível do coeficiente de atrito, ocorre justamente na igualdade:
Como kg, kg, , ficamos com:
Prontinho galera, finalizamos mais uma questão! Espero que vocês tenham aprendido bastante.
Até a próxima 😉
Resposta
a)
b)
c)
d)
e)