1) O mecanismo ilustrado na figura abaixo é constituído por 3 componentes: 1) um suporte ABOD (desenhado em azul) vinculado à articulação A e ao mancal radial B, que gira com velocidade angular constante em torno do eixo vertical; 2) uma luva C (desenhada em verde), que desliza ao longo da haste OD do suporte ABOD com velocidade constante relativa à haste; 3) um disco de raio R, solidário à luva C que gira em torno da haste OD com velocidade angular constante . O sistema de referência móvel é ligado ao suporte ABOD e, no instante mostrado na figura, o ponto P da periferia do disco encontra-se na posição . Nota: Todas as respostas devem ser expressas no sistema de coordenadas .

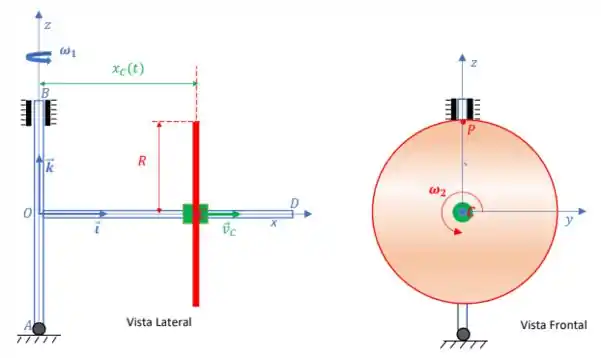
Pedem-se:

a) A velocidade absoluta do ponto C.

b) A aceleração absoluta do ponto C;

c) O vetor rotação absoluta do disco;

d) O vetor aceleração rotacional absoluta do disco;

e) A velocidade absoluta do ponto P;

f) A aceleração absoluta do ponto P.

b) Agora devemos determinar a aceleração absoluta do ponto C.

Beleza! Aqui temos um caso complicado de aceleração porque há muitos movimentos na composição, além de que o sistema de referência é móvel o que gera uma aceleração de coriolis. Mas calma, a gente só precisa aplicar o método!

Em casos complexos como esse, devemos usar a seguinte fórmula para cálculo da aceleração absoluta:

Onde:

aceleração do ponto C em relação ao sistema móvel.

: aceleração do ponto C’ do corpo rígido que coincide com a partícula C (nesse caso, nossa luva) no instante considerado.

: aceleração de Coriolis.

Ótimo, reduzimos o nosso problema a outros 3 problemas menores. Vamos calcular cada uma dessas acelerações separadamente:

1) Cálculo de :

Esse primeiro caso é bem tranquilo, porque o sistema móvel também está girando junto com o ponto C. A única diferença nos movimentos, é que a luva está transladando na haste OD com velocidade constante .

Mas pensa comigo, se estamos interessado na aceleração relativa, e o único movimento do ponto C (diferente da rotação do sistema móvel) possui velocidade constante, a aceleração relativa é nula. Certo? Conseguiram pegar a ideia?!

2) Cálculo de :

Aqui temos a composição de dois movimentos. É como se fosse a aceleração que usaríamos caso não tivéssemos um sistema de referencial móvel girando, gerando também uma aceleração de coriolis. Ou seja:

Como é constante, é nulo. Além disso, o ponto da origem do sistema móvel tem aceleração nula, daí:

3) Cálculo de :

Sabemos que a aceleração de coriolis pode ser calculada pela fórmula:

Mas, a velocidade relativa de C ao sistema móvel é apenas a velocidade do movimento de translação, daí:

Substituindo, temos:

Aeee, finalmente encontramos tudo. Agora é só substituir na nossa fórmula geral da aceleração:

Prontinho 😊

c)

Aqui precisamos calcular o vetor rotação absoluta do disco.

Basicamente, a ideia é que precisamos considerar todos os movimentos de rotação realizados pelo disco para encontrar o vetor rotação.

Devido ao movimento do próprio disco, ele rotaciona em torno de C com .

Já devido ao movimento de rotação da haste OD, o disco também está rotacionando em torno do eixo , com velocidade angular .

Beleza, agora é só somar.

d) Devemos calcular o vetor aceleração rotacional do disco. Para isso, basta usarmos nossa fórmula:

- é a derivada da velocidade relativa do ponto do corpo rígido onde o disco está no instante considerado. Mas, como é constante, essa derivada é nula. Logo: .

- é a derivada da velocidade relativa do disco no seu movimento de rotação próprio. Mas, novamente, como é constante, essa derivada é nula. Logo: .

-

Logo:

Calma galerinha, só faltam duas letras. Estamos quase lá!

e) Aqui precisamos determinar a velocidade absoluta do ponto P. A ideia é usarmos alguns resultados que já calculamos anteriormente pra facilitar nosso trabalho.

Pensa comigo, uma das melhores formas que temos de calcular é:

Essa forma é muito boa porque já conhecemos do item (a). Daí:

Por fim:

f)

Devemos calcular a aceleração absoluta do ponto P. Nesse caso, também podemos usar o ponto C para nos dar uma ajudinha, pois já calculamos a aceleração absoluta desse ponto. Daí, podemos fazer:

Substituindo os valores de , e que já encontramos nos outros itens, como também que , ficamos com:

Muita conta né?! Eu sei ☹. Mas não tem muito pra onde correr, é respirar fundo e dar o gás final nessa questão.

Resolvendo essas continhas padarianas (só que não), chegamos a:

Conseguimos galeraaa!! Finalmente terminamos essa questão. Agora é beber uma água, descansar um pouquinho, e partir pra próxima!