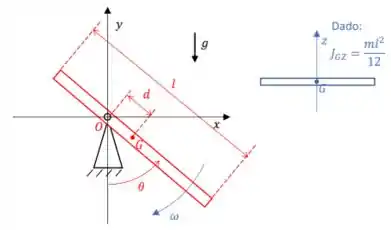
2) Uma barra delgada e homogênea, de comprimento e massa é articulada em a uma distância do seu centro de massa, estando restrita a mover-se no plano , conforme ilustrado na figura.

a) Determine o momento de inércia da barra.

b) Sabendo que a barra parte da posição angular com velocidade angular inicial no sentido horário, determine o menor valor de em módulo, para que a barra não mude o sentido de rotação

b) Primeiro vamos entender o que a questão está nos pedindo. Imagina que a barra começa a realizar o movimento de rotação dela em torno do ponto , existem duas possibilidades possíveis: Ou a barra consegue realizar uma rotação completa e permanece girando no sentido horário, ou ela não tem energia suficiente e em algum momento da volta ela vai inverter o seu sentido de giro.

Nesse item, devemos calcular o menor valor de para que ela consiga realizar uma oscilação completa, ou seja, não inverta o sentido do giro. Beleza? Pegaram a ideia?

Ou seja pessoal, esse é um problema de energia. A barra precisa ter energia inicial suficiente. Sendo assim, vamos utilizar o teorema da energia cinética para a barra. Nesse caso, a única força fazendo trabalho é o próprio peso da barra.

Daí, vamos ter a seguinte equação:

A condição para haver inversão de movimento, é termos . Isso, inclusive, é uma dica sempre questões perguntam sobre momentos de altura máxima, ou onde ocorre inversão de movimento, devemos ter ou a velocidade linear, ou a velocidade angular (ou ambas) iguais a zero.

Usando a nossa condição na equação, teremos:

Agora é só tirar a raiz e correr pro abraço:

Esse é o menor valor possível de que garante que a barra irá realizar a rotação completa, ou seja, não inverterá o sentido do movimento.