3) A figura abaixo representa um dispositivo robótico movendo-se num plano vertical, com aceleração da gravidade . Na extremidade A da coluna fixa há um pequeno motor elétrico que aplica um momento (anti-horário) na extremidade A do braço AB, fazendo este braço girar em torno de A com velocidade angular e aceleração angular , dados. Na extremidade B do braço AB há outro pequeno motor, que aplicar o momento (anti-horário) no braço BC, fazendo-o girar com velocidade angular e aceleração angular A massa do braço AB é , a do braço BC é e ambos podem ser considerados como hastes delgadas homogêneas.
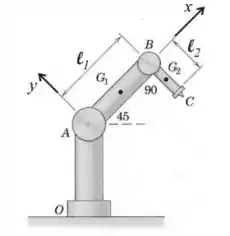
Para a posição indicada na figura, e usando o sistema de eixos indicados, pede-se:
a) Desenhar os diagramas de corpo livre dos braços AB e BC;
b) Escrever as equações do teorema da resultante (TR) e do Teorema da quantidade de movimento angular (TQMA) para o braço BC;
Supondo que o motor em B trave a conexão dos braços AB e BC na posição relativa mostrada, pede-se:
c) obter as expressões de e em função de , das massas e das dimensões dadas na figura;
d) Determinar o momento exercido pelo braço AB sobre o braço BC.
Passo 1
Ooi gente, tudo bem com vocês?
a) Bom, pra começar essa questão precisamos desenhar os diagramas de corpo livre (DCL) dos braços AB e BC.
É importante nos atentarmos às forças nos pontos A e B, principalmente. É como se as barras estivessem articuladas nesses pontos, de modo que deve haver reações e . Outro detalhe importante, é no DCL da barra AB, as reações (inclusive o momento no ponto B devem estar em sentido oposto ao desenhado no DCL da barra BC, para que haja o equilíbrio do nó B. Por último, não podemos esquecer de colocar os pesos das barras, agindo bem no meio delas.
Pronto, se atentando a esses pequenos detalhes, chegamos aos seguintes diagramas:
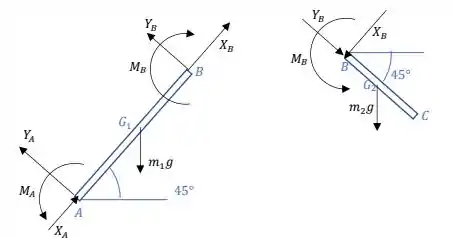
Eaí, entenderam bem? Bora pra próxima!
Passo 2
b) Nesse item precisamos escrever tanto as equações do teorema da resultante (TR), como do teorema da quantidade de movimento angular (TQMA) para o braço BC.
Começando pelo teorema da resultante, no caso geral, ele diz o seguinte:
Daí, quando a massa é constante, ela pode ser tirada da derivada, e ficamos com:
Beleza, então vamos escrever essa equação vetorial, observando sempre o DCL da barra BC.
Boa! Já matamos uma parte do item.
Indo agora para o TQMA, ele fala que:
No caso da nossa barra BC, temos que o momento angular em vale:
Logo:
Já quando ao momento em , temos:
Juntando tudo, temos que:
Prontinho pessoal, é isso aí!
Passo 3
c) Precisamos calcular e em função dos dados.
Aqui tivemos uma suposição bem interessante que restringiu mais a cara desse problema. Segundo o enunciado, devemos agora considerar que as barras AB e BC estão travadas na posição mostrada na figura.
Beleza, mas e aí né? O que isso muda no que já fizemos até agora?
A ideia é que, se AB e BC estão travadas é porque elas estão girando sempre juntas. Ou seja:
Massa! Para encontrar podemos usar o ponto A como referência, daí:
Como A é um ponto fixo, e usando as dimensões do enunciado, temos que:
Lembrando que e são dados. Portanto, já determinamos também . Falta apenas .
E a ideia aqui é usar um raciocínio semelhante, vamos determinar usando A como referência, e depois usando B como referência. Daí:
Ficamos com:
Perfeito, temos então para :
Muito bomm! Esses produtos vetoriais enchem o papel de conta, mas são bem úteis né?!
Passo 4
Bora lá pessoal, última item dessa questãozinha! Hora do gás final pra aprendermos a última ideia.
d) Precisamos calcular quanto que vale o momento , pois ele é justamente o momento que o braço AB exerce sobre o braço BC, como pudemos verificar no DCL.
Daí, se usarmos a nossa TR do item b, temos que:
Mas usando o resultado encontrado no item c, temos que o mesmo vale:
Igualando as duas equações, vem que:
Agora que já temos o valor de , podemos ir na nossa equação do TQMA do item b. Vamos ter que:
Logo, substituindo e isolando o , vem:
Por fim:
Ufaaa! Conseguimos terminar mais uma! Questão bem interessante com uso do TR e do TQMA, vale a pena guardar as ideias! Obrigado pela atenção pessoal, tmj!
Resposta
a) Resolução no texto
b) Resolução no texto
c) Resolução no texto
d)