02) Considere o sistema ilustrado na figura, em que os discos e , de centros e , respectivamente, são vinculados entre si por meio de uma articulação ideal localizada na periferia de ambos, em . Há ainda, em , uma articulação que vincula o disco a uma base fixa com respeito a um referencial inercial. Denote por e as respectivas acelerações angulares dos discos e . Admita que os discos são idênticos, homogêneos e têm massa e raio . Para a configuração indicada na figura, em que as linhas e estão na vertical e horizontal, respectivamente, e admitindo que os discos encontram-se inicialmente em repouso, pede-se, para o instante imediatamente após a liberação do sistema:
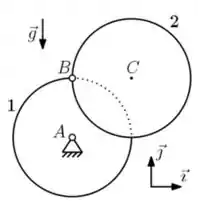
a) Os diagramas de corpo livre para cada um dos discos.
b) As expressões das acelerações dos pontos e em função de e .
c) Os valores de e .
d) A força aplicada pelo disco de centro sobre o disco de centro por meio da articulação em .
Dado: para o disco de centro ,
Passo 1
Eaí galerinha, bora matar mais uma questão de mecânica!!
Nesse exercício temos dois discos que estão articulados entre si no ponto . O disco também está articulado no seu centro, de modo que está fixo. Além disso, é importante perceber que eles estão no mesmo plano da gravidade, ou seja, há foça peso agindo sobre eles.
a) Beleza, no item a) precisamos desenhar os diagramas de corpo livre (DCL) de cada disco.
Pra desenhar DCL a o bizu é sempre começar identificando as forças que agem no corpo.
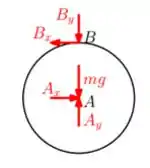
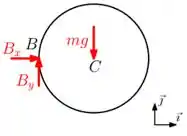
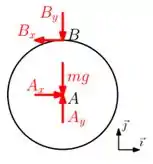
Assim, no disco , temos as reações em e em devido à articulação em e em , a força peso atuando no centro do disco, ou seja, em . Daí:
Massa! Já o disco é praticamente a mesma coisa, mas ele não está articulado no seu centro, o ponto . Por isso, só tem as reações e atuando em . Inclusive, é importante termos cuidado aqui, como o ponto precisa estar em equilíbrio, devemos ter e atuando em sentidos opostos aos que desenhamos no disco , sacaram? Logo:
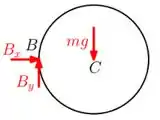
Excelente, bora pro próximo 😊
Passo 2
b) Agora devemos determinar expressões para e em função de e .
Nesse tipo de situação tem uma equação da cinemática que sempre usamos, vocês lembram qual é?

É a equação da aceleração em um movimento plano geral. Para o ponto , por exemplo, ela nos permite escrever que:
Essa é a expressão geralzona, onde e são a aceleração e velocidade angular, respectivamente, de em torno de .
Só que, no nosso caso, temos uma situação imediatamente após o sistema sair do repouso, ou seja, podemos considerar . Como é um ponto fixo, . Pela figura abaixo, também vemos que:
Substituindo tudo na equação de , temos:
Show! Vamos agora calcular usando o mesmo tipo de equação, mas usando como apoio:
Mas, novamente temos . Pela figura abaixo, também podemos escrever que:
Substituindo tudo em , vem:
Bouaa! Conseguiram pegar a ideia? É bem comum esse tipo de pergunta nas questões de mecânica.
Passo 3
c) Nesse item precisamos determinar e .

Calma galera, parece ser bem complicado, mas o trabalho é mais conta mesmo. Como já usamos as equações da cinemática, agora é hora de recorrer às equações da dinâmica!
Bora invocar o teorema da resultante e o teorema da quantidade de momento angular (TQMA) 😊
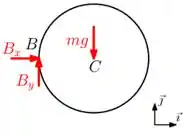
Começando pelo teorema da resultante, para o disco , temos:
Para o disco :
Assim:
Logo, temos:
Assim:
Também vale:
Boa!
Passo 4
Agora vamos aplicar o TQMA, colocando o polo em para o disco .
Puts, tem um problema: pelo dado da questão só conhecemos o momento de inércia em relação ao eixo do disco, ou seja:
Pra calcular devemos usar o teorema dos eixos paralelos:
Massa! Daí agora é só substituir na equação do TQMA, junto com os outros dados que já determinamos. Vem que:
Logo:
Muito bom! O primeiro já foi haha. Usando o TQMA para o disco , colocando o polo em , temos:
Pelo dado da questão, sabemos que:
Assim:
Substituindo o valor de que encontramos anteriormente, vem:
Ué, que estranho né? Isso só quer dizer uma coisa...

Pô, bem surpreendente né? Encontramos que o disco está rotacionando, enquanto o disco está parado. Pelo menos no instante imediatamente depois do início do movimento, é isso mesmo.
Passo 5
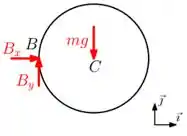
d) Pra finalizar vamos calcular a força que o disco de centro aplica no disco de centro através da articulação em .

Hahaha, o enunciado complicou mas basicamente é só calcular a força resultante das reações que aplica em no disco de centro . Ou seja:
Substituindo os resultados que encontramos no passo , vemo:
Mas, como:
Temos:
Ufaaa, todo mundo vivo até aqui?
É isso, matamos mais uma questão, até a próxima pessoal!! 😉
Resposta
a) Resolução no texto.
b)
c)
d)