03) Um disco homogêneo, de massa e raio , pode rolar sem escorregar sobre uma superfície plana horizontal que está fixa com respeito a um referencial inercial. A mola linear, de rigidez e comprimento natural , está vinculada a uma base fixa em e ao disco em seu centro . Seja o ângulo entre e a vertical , indicado na figura. Pede-se:
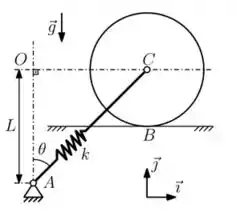
a) O diagrama de corpo livre para o disco.
b) As expressões, em termos de e , do vetor posição , da velocidade do ponto e da velocidade angular do disco.
c) A expressão da energia cinética do sistema.
d) A expressão da energia potencial do sistema.
e) Considerando que o sistema parta do repouso na configuração , determine o vetor de rotação do disco quando o sistema atingir pela primeira vez a configuração .
Dado: para o disco,
Passo 1
Faaaala galerinha do bem, como vocês estão?
Essa questão é bem interessante, o enunciado dela traz algumas informações meio escondidas, então vamos analisar com calma.

Basicamente, temos um disco cujo centro está preso a uma mola alongada. Esse disco se apoia em uma superfície, e rola sem escorregar.
Essa última informação é fundamental, pra um disco rolar sem escorregar a velocidade tem que ser nula no ponto de contato, ou seja, em . Isso só vai acontecer se existir um atrito agindo nesse ponto. Assim, como o disco está transladando na direção ) devido à força elástica, o atrito aponta na direção .
Tudo isso enquanto também rotaciona com centro instantâneo de rotação em B.
a) O objetivo desse primeiro item é determinarmos o diagrama de corpo livre (DCL) do nosso disco.
O bizu pra desenhar DCL é começar identificando as forças que agem no corpo.

No caso do nosso disco, temos a força peso agindo no seu centro , a normal e o atrito agindo no contato , e também a força elástica da mola puxando o disco através do ponto . Logo:
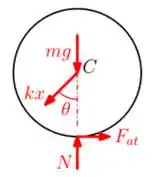
Massa!!
Passo 2
b) Aqui devemos calcular o vetor posição , a velocidade do ponto e a velocidade angular do disco em função de e .
Bora começar por . Usando as direções e , temos:
Onde representa a distância horizontal entre e . Daí:
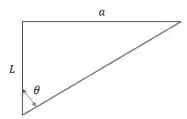
Pela figura acima, sabemos que:
Logo:
Massa! Pra determinar a velocidade do ponto , podemos derivar o vetor posição. Assim:
Portanto:
Bouaa! Pra terminar esse item só precisamos determinar a velocidade angular do disco.
Mas pô, não apareceu velocidade angular em nenhuma dessas equações, e agora?

A sacada é lembrar que é centro instantâneo de rotação, assim também podemos escrever:
Igualando as duas expressões, temos:
Prontinho 😊
Passo 3
c) Devemos determinar a energia cinética do sistema.
O problema é que esse disco tá rolando, será que dá pra ignorar esse fato?

Nãaao, né pessoal? Precisamos considerar a energia cinética como sendo a soma de duas parcelas:
Assim, lembrando que:
Logo:
é dado e vale . Substituindo os dados, vem:
Por fim:
Passo 4
d) Agora vamos determinar a expressão da energia potencial do nosso sistema.
Basicamente, vamos ter dois tipos de contribuição: , .
Assim:
Bora começar calculando a parcela elástica. Ela segue a fórmula:
Onde é a deformação da mola.
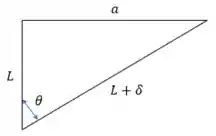
Assim, temos:
Substituindo na nossa expressão para a energia, vem:
Massa! Já o caso da é um pouco diferente. O que acontece é que em geral não calculamos um valor absoluta dessa energia, mas sim uma variação em relação a um certo nível de altura convencionado como referencial.
Só que, como o disco rola sobre a superfície, o seu centro sempre estará à mesma distância de qualquer nível que convencionarmos como referencial. Sendo assim, durante o movimento não haverá variação de e podemos considerá-la nula desde o início 😊
Portanto:
Bouaa! Já vamo pro último item!!
Passo 5
e) Pra encerrar a questão, precisamos determinar o vetor rotação do disco, , quando o disco passa pela primeira vez na posição , sabendo que .
Um negócio legal de perceber é que, se a superfície tiver comprimento longo o suficiente, o disco irá realizar um movimento oscilatório, tipo um .

Bom, voltando à questão, precisamos ter um pouco de malandragem também. Pelo enunciado vemos que os itens estão nos direcionando para uma abordagem por energia, então é isso que vamos fazer!
Bora olhar o DCL do disco:
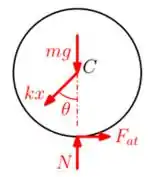
Temos basicamente forças atuando. Quais delas realizarão trabalho?

Beleza, a normal nunca realiza trabalho! O peso só realiza trabalho se tiver deslocamento vertical, o que não ocorre. Agora cuidado:
O atrito até realizaria trabalho, mas como o disco rola sem escorregar, o ponto em que o atrito está agindo está sempre com , é como se ele estivesse parado a cada instante, de modo que o trabalho do atrito é nulo também. Sacaram?

Portanto, só nos resta a força elástica, que é uma força conservativa. Assim, podemos conservar a energia entre o instante inicial e o final. Daí:
Usando que , e também que o sistema ainda está em repouso, vem:
Quando tivermos , temos que vale:
Igualando as duas expressões, chegamos que:
Logo, isolando , vem:
Como o disco rola para a esquerda, , assim:
Mas, sabemos lá do item b), que:
Substituindo, finalmente temos que:
Aeeee, matamos mais uma! Essa abordagem por energia é bem interessante né?
Valeu galera, até a próxima! Tamo junto 😊
Resposta
a) Resolução no texto.
b) Resolução no texto.
c)
d)
e)