Uma bala de é disparada horizontalmente com uma velocidade contra o bloco de de madeira macia inicialemnte em repouso sobre a superfície horizontal. A bala emerge do bloco com a velocidade , e se observa que o bloco desliza uma distância de antes de parar. Determine o coeficiente de atrito dinâmico entre o bloco e a superfície.
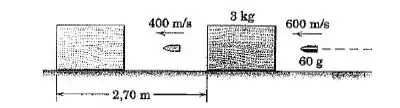
Passo 1
O momento se conserva? Sim:
O momento inicial é dado por:
E o momento final? No fim, o bloco de tem uma certa velocidade, assim como a bala:
Assim:
Passo 2
Bom, descobrimos que após o impacto da bala o bloco tem uma velocidade de .
No entanto, depois de um tempo, o bloco para. Vamos usar o teorema trabalho-energia pra calcular o coeficiente de atrito
Assim:
Onde . E a normal? A normal é igual ao peso para que seja assegurado o equilíbrio vertical:
Assim:
Passo 3
E a variação da energia cinética? Ela é dada por:
Igualando: