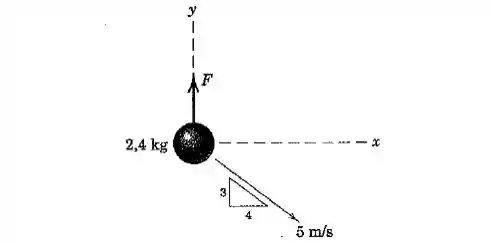
A partícula de se desloca no plano horizontal xy e tem a velocidade mostrada no instante de tempo . Se a força newtons, onde é o tempo em segundos, é aplicada à partícula na direção y iniciando no instante de tempo , determine a velocidade da partícula 4 segundos após ser aplicada e especifique o ângulo correspondente medido no sentido anti-horário a partir do eixo x até a direção da velocidade.
Passo 1
Vamos primeiro calcular as componentes e da velocidade inicial:
Perceba que o cosseno e o seno do triângulo retângulo mostrado valem:
Assim:
Assim:
Passo 2
Perceba que a força atua apenas na direção Sendo assim, apenas haverá uma mudança na componente vertical da velocidade:
Assim:
Passo 3
Assim, a velocidade final da partícula será:
E o ângulo será:
Resposta
Exercícios de Livros Relacionados
Uma batata de massa 0,5 kg se move sob a gravidade da Terra, com uma força resistiva do ar igual a -kmv.Determine a velocidade terminal caso a batata seja liberada do repouso e k = 0,01 s-1.Determine
Uma bola de 1k g está viajando horizontalmente a 20m / s quando atinge um bloco B de 10k g que está em repouso. Se o coeficiente de restituição entre A eB é e = 0,6 e o coeficiente de atrito cinético
O bloco de 10k g está parado sobre a superfície horizontal quanto a força T é aplicada a ele por 7 segundos. A variação de T com o tempo é apresentada. Calcule a velocidade máxima atingida pelo bloco
O tampão cilíndrico A de massa m A é liberado a partir do repouso em B e desliza para baixo na guia circular lisa. O tampão atinge o bloco C e se encaixa nele. Escreva a expressão para a distância s q
O módulo de aterrissagem lunar de 200k g está descendo na superfície da Lua com uma velocidade de 6m / s quando seu retromotor é acionado. Se o motor produz um empuxo T por 4s que varia com o tempo co