Calcule o limite abaixo usando as propriedades operatórias:
Passo 1
Faaala! Como estão os estudos? Decolando?!
Se liga! Esse é um exercício de limite. Qual é o primeiro passo de todo exercício de limite?
Isso aí. Substituir a variável pela tendência da variável! Nesse caso, a variável é o . A tendência da variável é valer . Logo, temos que substituir por :
É, deu ruim! O resultado dessa substituição foi uma divisão de zero por zero . Xiiii, não é possível dividir um zero por zero! Essa divisão é uma indeterminação. Vamos ter que encontrar um outro método de solução!
Passo 2
Se tentarmos descobrir o que deu errado nessa substituição de por , veremos que a culpa de tudo é da parte de baixo da fração ! Como , quando , o resultado vira uma divisão por zero impossível de ser calculada! Logo, antes de substituir por , temos que nos livrar do que está embaixo da fração!
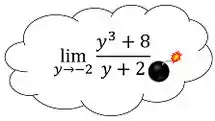
Para o desaparecer da parte de baixo da fração, temos que fazer aparecer na parte de cima ! Se fizermos isso, vamos poder cortar o debaixo com o de cima! Em outras palavras, temos que reescrever a parte de cima da equação de forma que apareça .
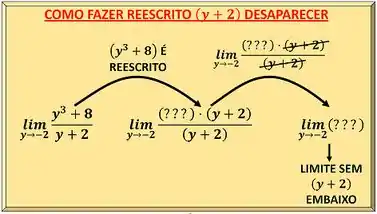
Fazemos isso através de um produto notável que não é muito comum, mas será bem útil para o que estamos precisando.
Isso pode funcionar para o nosso caso, porque o termo do limite se parece muito com o termo do produto notável! Olhando rápido você pode achar que os dois não se parecem, porque em existem dois números elevados ao cubo ( e ) e em apenas o está elevado ao cubo. No entanto, se a gente se lembrar que :
Usando essa informação, fica mais fácil de ver quanto e valem para o nosso caso.
Como já sabemos quem está no lugar do e do , vamos reescrever o produto notável no mesmo formato, mas agora trocando o por e o por :
Usando esse produto notável, a gente consegue reescrever e, de quebra, fazer o termo aparecer na parte de cima da fração!
Agora vamos reescrever o limite e ver se isso nos ajudor na hora de substituir por novamente.
Passo 3
Reescrevendo, ficamos com isso aqui:
Com isso podemos cortar o da parte de cima e da parte de baixo.
Ficando apenas com:
Substituindo novamente por , podemos achar o valor certo do limite sem nenhuma indeterminação para nos atrapalhar!
Parabéééns! Mais um exercício concluído! Vamos que vamos!