Calcule o limite, se existir.
Passo 1
Podemos pensar em calcular esse limite apenas substituindo o valor na expressão, entretando, ao fazer isso, ficamos com a inderterminação , observa.
Aí não dá pra trabalhar, né? Então fazemos o que? Vamos então fazer manipulações para tirar essa indeterminação, só analisar um pouco e vamos descobrir, calma que vai da certo!
Passo 2
Vamos tentar manipular o numerador, resolvendo a expressão elevada ao quadrado:
Um número ao quadrado é como se fosse ele vezes ele mesmo, certo? Então vamos fazer isso
Pra resolver essa multiplicação precisamos lembrar da multiplicação de polinômios
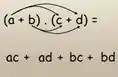
Nesse caso, nosso
Agora podemos colocar o em evidência e simplificar com o do denominador, vamos lá:
Passo 3
Pronto, agora é simples, só substituir o valor na expressão: