Calcule o limite:
Passo 1
Opa fala aii! Vamos continuar com nossos limites!
A gente começa substituindo o limite, certo?
Deu ruim né? Então, vamos tentar dar um jeitinho algébrico.
Passo 2
Zerou em cima e embaixo, o que significa que vai aparecer na fatoração dos dois termos.
Vamos dividí-los por esse termo, o de cima por Briot-Ruffini, o de baixo por Bhaskara.
Começamos com o de baixo, que é mais tranquilo
Para achar quem é e vamos lembrar da nossa forma da equação do segundo grau
E nossa equação é
Então temos que
Colocando isso no nosso Bhaskara, temos
Então temos duas raízes
Simplificando, temos que
Lembrando que para a equação
Podemos abrir ele comas raízes, e escreve-lo desse jeitinho aqui
Dessa maneira, abrindo o polinômio ele fica assim:
Como temos que , e
Temos
Passo 3
O de cima, dividimos ele por pelo método de Briot-Ruffini, lembrando que a gente tem um esquema para fazer esse Briot-Ruffini ai,
O esquema do Briot-Ruffini :
- Colocar uma raiz no coeficiente
- Colocar os coeficientes
- Desce o primeiro coeficiente
- Multiplica ele pela raiz
- Soma com o próximo coeficiente
- e assim por diante:
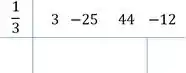
Desce o primeiro coeficiente:
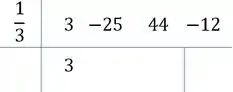
Multiplicamos a raiz pelo primeiro e somamos ao segundo:
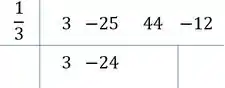
Repetimos isso para os dois outros números que restam:

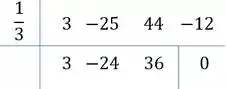
Ou seja,
Passo 4
Substituindo no limite:
Podemos cortar esse e ficamos com:
Aaaaaaaaaaah agora sim, podemos substituir felizes!
Dando uma penteada nele, ficamos com
Simplificando isso daí, temos
Fazendo essas somas, temos
Na divisão de 2 frações, repetimos a primeira e multiplicamos pelo inverso da segunda:
Aplicando o MMC, achamos que:
Que dá
Simplificando, temos