Calcule o limite, se existir.

Bom galera, para começar vamos adaptar um pouquinho! Basta multiplicarmos numerador e denominador por . Lembra daquele papo de multiplicarmos pelo conjugado? Fazemos isso com o objetivo de sumir com aquela raíz dali, afinal ninguém gosta de trabalhar com raiz, né? Então haha

Observa por qual razão fazemos isso

No nosso caso,

Observa que agora conseguimos nos livrar da raíz

Vamos também fazer uma multiplicação distributiva com esse que ta na parte do numerador.

Agora vamos aplicar o limite usando algumas propriedades. E vamos começar com:

Logo o limite pode ficar em cima e embaixo:

Outra propriedade é:

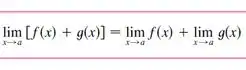
Assim essa parte de baixo cheia de somar pode ficar:

Usando a outra propriedade (kkkkk quantas propriedades). Tudo isso ajuda a gente a manipular nosso limite pra parar em algo que nós consigamos trabalhar sem cair em nenhuma indeterminação. Então lá vai:

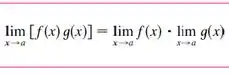
Vamos usar essa pra multiplicação do

Agora vamos usar a propriedade que nos permite trabalhar com o limite dentro da raíz.

Obs: Perceba que só foi possível fazer isso porque a raiz está em todos os elementos dentro do limite.

Gora o grande lance é cortar esse que ainda ta zerando tudo, e para isso vamos aIsolar colocando ele em evidência no denominador:

Agora cortamos o em cima e embaixo ficando com:

Por último

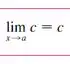
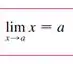
Ufa!!! Aí está esse danado!