Calcule o limite:
Passo 1
Tudo certinho? Tá arrebentando nos exercícios? Então bora partir para um novo desafio!
Como em todo exercício de limite, o nosso primeiro passo deve ser substituir pela tendência de . A tendência de é valer . Logo, temos que substituir por . Mas espera aí! O que aquelas barras que aparecem na parte de baixo do limite significam?

Essas barras são o módulo. O termo da equação é lido como: “o módulo de ”.
E o que o módulo faz de diferente?
O módulo é o seguinte: caso o termo que estiver dentro do módulo seja negativo, o módulo o fará ficar positivo. Mas se o termo que está lá dentro já for positivo, o módulo o manterá positivo.
Mas como ele faz isso???? Vamos ver um exemplinho pra dar aquela clareada nas ideias. Para isso vamos usar outro valor qualquer, tipo o 5:
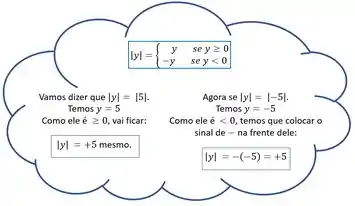
No nosso balazinho, o foi multiplicado por pra ficar positivo, por isso colocamos esse menos na frente dele.
Agora vamos ver como fica para o nosso exercício.
No nosso caso, o termo que está dentro do móludo é o . E saberemos que ele é negativo se ele for menor que zero. Então:
Por outro lado, se o termo que estiver dentro do módulo for maior ou igual a zero, o módulo não faz esse termo mudar!
Agora que entendemos o que o módulo significa, podemos substituir por !
Passo 2
Finalmente fazer a substituição de por ! Só que não!
Como o módulo se comporta de um jeito quando e de outro quando , precisamos fazer se aproximar de pela direita e pela esquerda .
Lembre-se que significa que se aproxima de por valores maiores que :

Lembre-se também que significa que se aproxima de por valores menores que :
Quando , o termo que está dentro do módulo será positivo
Logo ele vai ficar como veio ao mundo:
Quando , o termo que está dentro do módulo será negativo, pois
Logo ele vai ganhar aquele menos na frente:
Passo 3
Depois se lembramos desses detalher, finalmente podemos substituir por e calcular o limite pela esquerda e pela direita, já que teremos que fazer os limites laterais.
Vamos começar com limite pela direita :
Como nesse caso, :
No entanto, ao fazermos as contas descobrimos que o resultado final dá em indeterminação !
Fazendo o limite pela esquerda , e .
No entanto, ao fazermos os cáculos descobrimos que o resultado final dá de novo em indeterminação !
O resultado dessa substituição foi uma divisão por zero . Não é possível dividir um número por zero! Essa divisão é uma indeterminação. Por isso, esse resultado não serve pra gente! No próximo passo vamos descobrir como driblar esse problema.
Passo 4
No passo anterior, vimos que o culpado pela indeterminação é a divisão por zero. Essa divisão só acontece, por causa da parte de baixo da fração (o zero só aparece na divisão por conta de ). Logo, antes de substituir por , temos que nos livrar do debaixo do limite!

Para o desaparecer da parte de baixo da fração, temos que fazer aparecer na parte de cima ! Se a gente fizer isso, vamos poder cortar o debaixo com o de cima! Ou seja, vamos reescrever de forma que apareça.
Fazemos isso através de um produto notável chamado de trinômio quadrado perfeito. Que o carinha que tem esse formatinho aí:
Isso pode funcionar para o nosso caso, porque o termo do limite se parece com o termo do produto notável! Você pode estar achando que os dois não se parecem, mas isso fica mais claro, quando a gente lembra que:
Substituindo isso em , podemos comparar os valover com o produto notável e achar que é e quem é :
Como:
Usando esse produto notável, a gente consegue reescrever e fazer o termo aparecer na parte de cima da fração!
Agora, vamos reescrever o limite e substituir por de novo.
Passo 5
Reescrevendo o limite através do produto notável, achamos:
Cuidado! Lembre que, como o módulo age de forma diferente quando e , precisamos calcular o limite duas vezes: uma vez pela direita e outra pela esquerda .
Começamos então com o limite pela direita.
Cortando o termo que existe em cima e embaixo, achamos:
Agora sim, substituindo por :
Agora, vamos calcular o limite pela esquerda.
Cortando o termo que existe em cima e embaixo, achamos:
Substituindo por :
Enfim, o limite lateral é igual pela esquerda e pela direita. Isso significa que o limite existe e vale !

É isso aí! Mais um exercício concluído, guerreiros!