Encontre a parametrização da curva dada equação
Respeitando a inequação
Passo 1
Vamos lá pessoal!
Essa curva aí é uma daquelas clássicas dada na teoria, lembra? Se não lembra, não tem problema, se liga aqui, quando falamos de elipse e circunferência geralmente temos essa fórmula aqui:
Nesse nosso caso não está igual a , né? Mas isso não é problema, é só dividir por dos dois lados, fica assim
E isso nos dá que
Agora nossa curva ficou com a cara de uma elipse. O esboço é esse aqui:
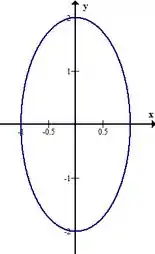
Pra saber como desenhá-lo você olha a raiz quadrada do valor do denominador que está embaixo de cada variável. Então no nosso caso, quem está embaixo o é o , e . Por isso ela corta o eixo nesses valores.
O mesmo vai acontecer com . Quem está embaixo dele é o , e . Assim, ela corta o eixo , nesses pontos.
Passo 2
Pra parametrizar isso aí a gente usa a relação fundamental da trigonometria
O formato é parecido com a nossa curva. Se chamarmos:
Temos que
Tirando a raiz dos dois lados das equações encontramos:
Como se trata se senos e cossenos, temos que:
Passo 3
Teoricamente essa seria a nossa resposta, só que a questão bota uma outra limitação ali, ela diz que
Ué, mas o que isso quer dizer? Pensa o seguinte, nessa elipse completa os limites de e são
A gente consegue ver isso no nosso gráfico!!
Existem pontos em que o produto de por não dá positivo (maior que zero). Poh, então como podemos garantir que de fato é positivo?
Bom, vamos ter que fazer um estudo de sinal aqui, pensa só, quando é positivo e é positivo, o produto também vai ser positivo! Agora, quando um é positivo e o outro negativo, o produto dá negativo. De forma geral é isso aqui
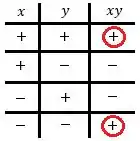
Então, para que , precisamos que e sejam positivos ou que ambos sejam negativos. E quando isso acontece? O plano é dividido em quatro quadrantes, vamos analisar cada um deles separadamente aqui
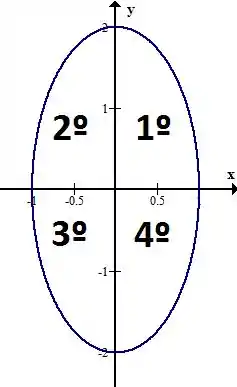
No 1º quadrante temos que , nessa região e são positivos, então o produto também é maior que zero
No 2º quadrante temos que , aqui é negativo e é positivo, então o produto é menor que zero
No 3º quadrante temos que , nessa região e são negativos, então o produto é maior que zero
No 4º quadrante temos que , nessa região é positivo e é negativo, então o produto é menor que zero
Portanto, somente no primeiro e no terceiro quadrante temos , então os limites de são