A análise do fluxo de um líquido em duto tem aplicação em muitos sistemas diferentes, incluindo o estudo em veias e artérias no corpo humano, o sistema hidráulico de uma cidade, o sistema de irrigação de uma fazenda, o sistema de jato de tinta de uma impressora, etc.
O atrito de um fluxo ao passar num oleoduto circular gera a chamada velocidade de perfil no fluido.
O óleo que está em contato com as paredes do duto não está se movendo na mesma velocidade que o óleo no centro do fluido. O diagrama abaixo mostra como a velocidade do óleo varia de acordo com o diâmetro do duto e define as variáveis usadas para esta análise:
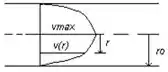
A velocidade de perfil é definida pela seguinte equação:
onde é um número inteiro entre 5 e 10 que define o contorno do escoamento do óleo. A velocidade média de escoamento do óleo pode ser calculada integrando-se a velocidade de perfil no intervalo de a :
Os valores de e de podem ser medidos experimentalmente, e o valor de é o próprio raio do tubo. Escreva um programa no MATLAB para integrar a velocidade de perfil e assim determinar a velocidade média do óleo no duto.
Conside , e .
Passo 1
O enunciado pede para encontrarmos a velocidade média de um óleo escoando em um duto de raio , com uma velocidade máxima de . Para isto, devemos resolver no MATLAB a seguinte integral:
onde
O resultado desta integral é a velocidade média do óleo. Devemos considerar .
Para calcularmos a integral do enunciado, podemos usar a função do MATLAB.
Passo 2
O primeiro passo é entrarmos com as informações do enunciado no MATLAB. Crie um script novo e digite as linhas de código:
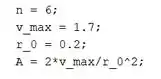
Criamos variáveis para armazenar os valores , e . Respectivamente, são as variáveis , e .
Em seguida, calculamos a constante , que é armazenada na variável .
O passo seguinte consiste em criar as entradas para a função .
Passo 3
Vamos criar o intervalo de integração com as seguintes linhas de código:
![]()
Na primeira linha, é criado um vetor que vai de a , com um passo de . O vetor representa o intervalo de integração pra encontrar a velocidade média do óleo no duto, lembrando que é o raio do duto.
Eu adotei o passo de para gerar um resultado mais preciso na integração mais pra frente, mas você pode adotar o passo que quiser. Só não se esqueça que o tamanho do passo tem impacto direto sobre a precisão da integração: quanto menor o passo, mais precisa é a integração numérica.
Na segunda linha de código, a função conta quantos elementos tem o vetor e armazena o resultado a variável .
Agora, vamos criar um vetor representando a função ser integrada: . Para isto, usaremos um laço , por meio das linhas de código abaixo:
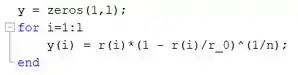
Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço pelo resultado de para cada elemento do vetor .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Concluído este passo, temos tudo o que precisamos para fazer a integração pedida no enunciado.
Passo 4
Para resolvermos a integral, usaremos a função que tem o seguinte formato:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
Este comando resolve a integral:
Para encontrarmos a velocidade média , temos que multiplicar o resultado da integral pela constante , que definimos lá no passo 2:
![]()
O produto corresponde à velocidade média do óleo escoando no duto, a qual é armazenada na variável .
Ao rodarmos o script do MATLAB, chegamos ao seguinte resultado:

O valor de é a resposta do exercício.
Resposta
A velocidade média do fluxo de óleo escoando por um duto de raio , com uma velocidade máxima de e considerando é de .