Com o software MATLAB, usando a Regra dos Trapézios, calcule as integrais das seguintes funções:
Passo 1
O exercício pede para usarmos o MATLAB para calcular a integral numérica de duas funções, usando a Regra dos Trapézios. Isto quer dizer que nos é pedido para usar a função do MATLAB, que calcula integrais usando o método dos trapézios.
Passo 2
A letra pede para calcular a integral da função:
Crie um script novo no MATLAB e entre com as duas linhas de código:
![]()
Na primeira linha de código, foi criado um vetor , que vai de a com um passo de . Este vetor representa o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Na segunda linha de código, o comprimento de foi armazenado na variável .
Agora vamos calcular a função para cada elemento de . Para fazermos isso, teremos que criar um laço , como no código abaixo:

Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço , sendo atualizado com o valor da função para cada valor de .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Com os vetores e definidos, já podemos calcular a integral da letra do exercício.
Passo 3
No passo anterior, foram criadas as duas entradas que precisamos para usar a função para calcular a integral da função. Lembrando que tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para a letra do exercício, inclua no seu script a seguinte linha de código:
![]()
A integral da letra é resolvida por meio desta linha de código, usando os vetores que criamos no passo 2. Ao rodarmos o programa, temos como resposta:

Lembre que se você usou um passo diferente de , seu resultado pode ser um pouquinho diferente, mas não significa que está errado. Você só dividiu a área sob a curva em partes de tamanho diferente do que eu fiz.
Pronto! Letra resolvida. Vamos fazer a letra .
Passo 4
A letra pede para calcular a integral da função:
Para resolvermos a letra , usaremos o mesmo passo a passo que fizemos para a letra . Em um novo script do MATLAB, digite as duas linhas de código:
![]()
De maneira similar ao passo 2, foi criado um vetor , que vai de a com um passo de , na primeira linha de código. Escolhi novamente um passo de , mas você pode usar o passo que quiser. Assim como no passo 2, este vetor representa o intervalo de no qual vamos integrar a função.
Na segunda linha de código, o comprimento de foi armazenado na variável .
Agora vamos calcular a função para cada elemento de . Novamente, vamos criar um laço :
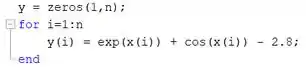
Este pedaço de código faz exatamente a mesma coisa que o pedaço de código com o laço apresentado no passo 2.
Primeiramente, é criado um vetor de zeros de mesmo comprimento de . Cada elemento de vai ser atualizado no laço com o valor da função para cada elemento de .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Executando este passo, já temos tudo o que precisamos para calcular a integral da letra do exercício.
Passo 5
Vamos usar a função para calcular a integral da letra . Inclua no seu código o comando:
![]()
Este comando vai retornar a integral da função , representada pelo vetor , para o intervalo representado pelo vetor . O resultado é armazenado na variável , que, aós rodar o código, equivale a:

Lembre que seu resultado pode ser um pouquinho diferente do meu, caso você tenha usado um passo diferente na criação do vetor .
Letra resolvida!