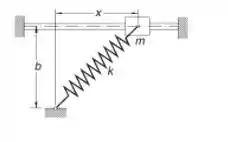
A massa é ligada a uma mola de comprimento livre e rigidez . O coeficiente de atrito entre a massa e a haste horizontal é . A aceleração da massa pode ser demonstrada como , onde
Se a massa é liberada a partir do repouso em , sua velocidade em é dada por
Calcule por meio de integração numérica usando como dados , , , e .
Passo 1
O exercício pede para calcularmos a velocidade resolvendo a equação:
Para encontrarmos antes temos que resolver a integral dentro da raiz, usando integração numérica. Para solucionar a integral, podemos usar a função do MATLAB.
O enunciado nos dá como dados:

Com os valores da tabela, podemos definir o intervalo de integração, que vai de a , e podemos calcular . Desta forma, temos as entradas de .
Passo 2
A primeira coisa que devemos fazer é entrar com os dados fornecidos pelo enunciado no MATLAB. Crie um novo script e digite as linhas de código:
Com estes comandos, entramos no programa os dados da tabela apresentada no passo 1. Chamei a variável que armazena o coeficiente de atrito de , que é uma das formas de pronunciar , já que não podemos usar letras gregas como nome de variáveis no MATLAB.
Vamos agora criar o intervalo de integração. Ele será representado por um vetor , construído com o comando:
![]()
O vetor vai de a , com um passo de . Eu adotei o passo de para gerar um resultado mais preciso na integração mais pra frente, mas você pode adotar o passo que quiser. Só não se esqueça que o tamanho do passo tem impacto direto sobre a precisão da integração: quanto menor o passo, mais precisa é a integração numérica.
Após ter digitado o comando para criar , adicione logo abaixo a linha de código:
![]()
Esta linha vai armazenar a quantidade de elementos do vetor na variável , por meio da função , que retorna o comprimento de um vetor. Precisamos do número de elementos de para podermos calcular usando um laço .
Agora, vamos criar um vetor representando a função ser integrada:
Como dito, usaremos um laço para isto, por meio das linhas de código abaixo:

Primeiramente, é criado um vetor de zeros de mesmo comprimento de , por meio do comando . Este vetor é chamado de e cada elemento dele vai ser substituído no laço pelo resultado de para cada elemento do vetor .
Em seguida, inicia-se o laço , criando-se uma variável de controle que vai de a . No bloco do , a função é calculada para cada elemento do vetor e o resultado é armazenado no elemento de mesma posição do vetor .
Concluído este passo, temos tudo o que precisamos para fazer a integração.
Passo 3
Para resolvermos a integral, usaremos a função que tem o seguinte formato:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Para nosso problema, o vetor entraria no lugar de e o vetor no lugar de . No seu programa, digite a linha de código:
![]()
Este comando resolve a integral:
Para encontrarmos , ainda precisamos fazer algumas continhas com o resultado da integral, armazenado na variável , retornada por . Lembre que é dado por:
No seu script, digite logo abaixo de a linha de código:
![]()
Esta linha calcula usando a expressão dada no enunciado e armazena o resultado em .
Ao executarmos nosso programa, temos o seguinte resultado para :

Resposta
A velocidade da massa em é de .