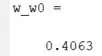A figura mostra um semi-espaço elástico que carrega um carregamento uniforme de intensidade sobre uma área circular de raio . O deslocamento vertical da superfície no ponto pode ser calculado como

onde é o deslocamento em . Use integração numérica para determinar em .
Passo 1
O exercício pede para calcularmos a razão usando integração numérica. Para determinar , basta resolver a integral, pois:
Para resolver a integral de forma numérica, podemos usar a função do MATLAB, que calcula integrais usando o método dos trapézios.
Passo 2
Em um novo script, crie o intervalo de integração com a linha de código:
![]()
Esta linha cria um vetor , que vai de a com um passo de , representando o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Passo 3
Em seguida, vamos calcular a função dentro da integral para cada valor do vetor . Podemos simplificar a função ao adotar :
Em seu script, implemente o cálculo de para cada valor de contido no vetor com a linha de código:
![]()
Os valores de para cada elemento de são armazenados no vetor .
Note o uso dos operadores e : eles indicam ao MATLAB que cada elemento de um vetor deve ser elevado ao quadrado e dividido pelo elemento de mesma posição no vetor do denomindor de uma divisão, respectivamente.
Passo 4
Nos dois passos anteriores, foram criadas as duas entradas que precisamos para usar a função para calcular a integral e obter : os vetores e . Lembrando que tem a sintaxe:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Inclua no seu script a seguinte linha de código:
![]()
Este comando resolve numericamente a integral e armazena em o resultado dela, que é a razão . Ao rodar o programa, vemos que é igual a: