Seja
Estime pela regra dos trapézios utilizando apenas os valores tabelados abaixo:

Passo 1
O exercício pede para resolvermos a integral com os valores da tabela, usando a regra dos trapézios.
Podemos fazer isso no MATLAB, usando a função , que permite calcular a integral numérica a partir de dados tabelados. A função terá como entrada a primeira linha da tabela, representando o intervalo de integração, e a segunda linha da tabela, representando .
Passo 2
O primeiro passo para resolvermos o exercício é entrarmos no MATLAB as informações dadas no enunciado. Crie um script novo no MATLAB e digite as duas linhas de código:
![]()
Na primeira linha de código, é criado um vetor que vai de a , com um passo de . Ele contém os valores da primeira linha da tabela e representa o intervalo de integração.
Na segunda linha de código, o vetor armazena os dados de apresentados na tabela.
Após criarmos esses dois vetores, temos tudo o que precisamos para usar a função .
Passo 3
A função do MATLAB tem a seguinte estrutura:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Neste exercício, o vetor entra no lugar de , pois representa o intervalo de integração, e o vetor entra no lugar de , já que representa para cada elemento do vetor .
Inclua no seu código o comando:
![]()
O comando vai calcular a integral e armazenar o resultado na variável .
Ao rodarmos o programa, temos como resultado:
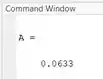
Resposta
A estimativa de pela regra dos trapézios utilizando apenas os valores tabelados é de .