A fórmula de Debye para a capacidade calorífica de um sólido é , onde
![]()
Os termos desta equação são
- número de párticulas no sólido
- constante de Boltzmann
- temperatura absoluta
- temperatura de Debye
Calcule de a em intervalos de e plote os resultados.
Passo 1
O exercício pede para calcularmos para diferentes valores de . Isto faz com que tenhamos que resolver a integral
várias vezes, para diferentes intervalos de integração, visto que define tal intervalo.
Por isso, usaremos a função dentro de um laço , para que a integral seja resolvida para cada valor de . A função também será calculada dentro do mesmo laço .
Ao final, plotaremos a curva de em função de com o comando .
Passo 2
Vamos começar definindo o intervalo de com o qual se deseja calcular . Em um script novo, digite o comando:
![]()
Este comando cria um vetor contendo os valores de com quais calcularemos . O enunciado pediu para fazermos indo de a , com um passo de . Por isso, o vetor vai de a , com um passo de .
Antes de iniciar o laço , vamos criar um vetor para armazenar o resultado de para cada valor de . Para isso, digite em seu script as linhas de código:
![]()
Na primeira linha, armazenamos na variável o número de elementos do vetor , por meio da função , que nos dá a quantidade de elementos de um vetor.
Na segunda linha, criamos um vetor composto só de zeros, com a mesma quantidade de elementos do vetor , por meio da função .
O vetor receberá o resultado de para cada valor de , tendo seus elementos atualizados dentro do laço .
Passo 3
Comece a implementar o laço , usando uma variável de controle que vai de 1 a .

Variando de a , conseguiremos acessar um a um todos os elementos do vetor por meio do laço . Também conseguiremos ir preenchendo o vetor , ao calcular dentro do laço e armazenando o resultado no elemento correspondente de .
Note que o intervalo de integração vai de a e o primeiro valor de é , o que dará um erro de divisão por . Por isso, precisamos incluir dentro do nosso uma condição para dizer ao MATLAB o que fazer quando . Quando , , por isso, inclua dentro do os comandos:

Desta forma, dizemos que se o elemento do vetor for igual a , o elemento do vetor também será igual a .
Caso seja diferente de , não haverá erro de divisão por no intervalo de integração. Por isso, é dentro do que faremos o cálculo da integral.
Passo 4
Para calcular a integral , precisamos definir o intervalo de integração, calcular para cada valor do intervalo e usar a função para calcular a integral. Lembrando que tem a sintaxe:
Ela nos retorna o resultado da integração, que representa a área sob a curva , definida no intervalo .
Por isso, após o dentro laço , digite as quatro linhas de código:

A linha
![]()
Cria um vetor , que vai de a , onde é o valor de na iteração , com um passo de . O vetor representa o intervalo de no qual vamos integrar a função. Escolhi um passo de para ter uma maior precisão no resultado, mas você pode escolher o passo que quiser. Mas lembre que quanto menor o passo, maior a precisão da integral numérica.
Na linha
![]()
Calculamos para cada elemento do vetor . Note os comandos , e , indicando que as operações são realizadas por elemento do vetor .
Na linha
![]()
Calculamos a integral. Contudo, perceba que eu não usei simplesmente e como entrada, mas sim e . Isto é, usei como entrada os dois vetores começando no seu segundo elemento. Fiz isso para não pegar o valor , pois , logo, o primeiro elemento de corresponde a (“not a number”, no MATLAB), o que não permite calcular a integral com .
Finalmente, na linha
![]()
Calculamos , multiplicando o resultado da integração pelo valor de da iteração elevalo ao cubo. O resultado é armazenado no elemento do vetor .
Desta forma, o laço está completo.
Passo 5
Para finalizar, vamos plotar o gráfico de em função de . Para isto, adicione as linhas de código:

Com a primeira linha, plotamos o gráfico do vetor em função do vetor .
Na segunda linha, dizemos que o eixo horizontal do gráfico corresponde a . Já na terceira linha, dizemos que o eixo vertical corresponde a .
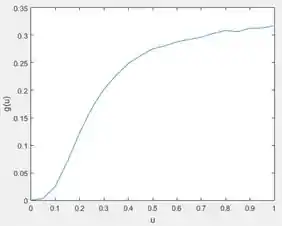
Execute o programa e você terá o gráfico pedido pelo exercício.
Resposta