Na mecânica dos fluidos, define-se camada limite como sendo a região de escoamento sobre uma superfície onde
(A) aplica-se a equação de Bernoulli
(B) as equações de conservação de massa, energia e quantidade de movimento não se aplicam
(C) não se aplica a equação de Bernoulli
(D) o escoamento é turbulento
(E) o escoamento é laminar
Passo 1
Faaaaala aí! Vamos analisar cada alternativa, mas antes vamos ter a camada-limite em mente? Ela pode ser representada assim:
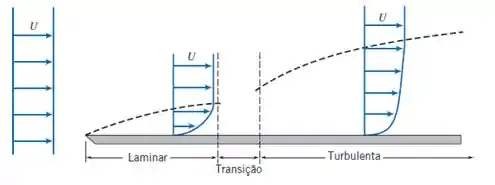
A camada-limite está relacionada a forças viscosas e de inércia. Ou seja, nela ocorre gradiente de velocidade (a velocidade varia), como mostrado na figura.
Já pela figura podemos ver que a camada-limite pode ser laminar ou turbulenta (o que vai depender do número de Reynolds).
Com isso, podemos eliminar as alternativas D e E, pois a camada-limite não é necessariamente turbulenta ou laminar por definição. Isso vai depender das características do fluido e do escoamento 😉
Ok! Vamos voltar a letra A. Nela, diz-se que na camada-limite necessariamente se aplica Bernoulli. Quando aplicamos Bernoulli isso quer dizer que não a perdas.
Esse não é caso da camada-limite, pois nela pode ocorrer perdas, uma vez que as forças viscosas são importantes nela. Essas forças estão associadas ao atrito interno e isso implica numa perda. Portanto, a letra A está errada.
Analisando a letra B: “as equações de conservação de massa, energia e quantidade de movimento não se aplicam”
Se as equações de conservação não se aplicassem na camada-limite Lavousier ia ficar muito bravo com a gente.

Hahaha Brincadeiras a parte: Nada se cria, nem se destrói, tudo se transforma. Na camada-limite não seria diferente!
Finalmente, a letra C diz que na camada-limite não se aplica Bernoulli. Essa alternativa está certa, pois justamente por sua definição, as forças viscosas e de inércia são importantes, o que leva a perdas e assim não se aplica Bernoulli.
Partiu próximo exercício? :D
Resposta
Alternativa C