Uma placa de madeira tipo compensado com dimensões de é colocada no topo de seu carro após ser comprada em uma loja de equipamentos. A que velocidade (em km/h no ar a 20°C) a camada-limite começará a ficar turbulenta? E em que velocidade a camada-limite é 90% turbulenta?
Dados: ,
Passo 1
Fala, aí! A primeira pergunta do exercício quer saber a velocidade numa situação crítica: quando o escoamento deixa de ser laminar e passa a ser turbulento. Como se trata de escoamento externo, precisamos definir valor de Reynolds crítico usar.
O escoamento do ar acontece numa placa de madeira (compensado). Ou seja, vamos considerar que a geometria é de uma placa plana lisa. Então:

Além disso, vimos na teoria que para o escoamento externo, essa equação é válida:
Então vamos substituir as informações do enunciado e o que acabamos de descobrir:
Quem seria o x, ou seja, a posição onde o escoamento sofre a transição de laminar para turbulento?
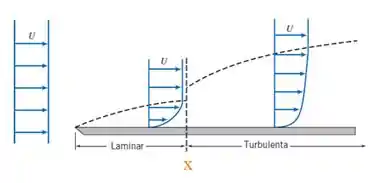
Vamos considerar que a placa foi colocada de tal forma que seu maior lado foi colocado na direção do movimento. Com isso, vamos assumir que esse ponto crítico x será no final do lado maior da placa, ou seja, x = 2.
Ali é onde ela vai começar a ficar turbulenta, que é justamente a condição do enunciado.
Assim, é possível calcular a velocidade
O exercício pediu a velocidade em km/h. Convertendo:
Passo 2
O exercício também pede a velocidade em que 90% da camada-limite é turbulenta.
A camada-limite está ao longo da placa, que tem 2 m de diâmetro. Para que 90% dela seja turbulenta, o ponto x crítico (onde a camada muda de laminar para turbulenta) deve ser nos primeiros 10% de comprimento da placa. Em matematiquês:
Substituindo
É 10 vezes a velocidade anterior, logo
Resposta
Situação 1
Situação 2