O circuito magnético mostrado abaixo tem as dimensões , e e espiras. Suponha o valor de para o material do núcleo. Dada a condição de que o circuito magnético esteja operando com , encontre:
as relutâncias e
o fluxo .
a corrente .
Passo 1
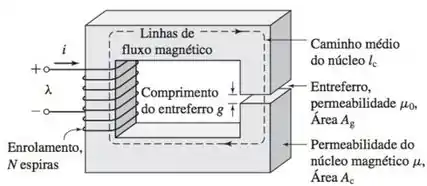
Neste exercício, além do núcleo de material magnético, temos um entreferro de ar. Quando o comprimento do entreferro é muito menor do que as dimensões da seção reta do núcleo, podemos considerar que não há dispersão do fluxo e utilizar as técnicas de análise de circuito magnético que conhecemos.
Temos que tomar com as unidades, tudo o que está em centímetros devemos passar para metros.
Além disso, foi dado a permeabilidade relativa do nucleo . Logo, a permeabilidade do núcleo é
Passo 2
A relutância do núcleo é calculada pela fórmula abaixo:
Logo, substituindo os valores:
Da mesma maneira podemos calcular a relutância do entreferro :
Passo 3
Como o fluxo que passa pelo núcleo é o mesmo que passa pelo entreferro, podemos calculá-lo utilizando a fórmula abaixo:
Substituindo os valores:
Passo 4
Para encontrarmos a corrente, primeiro, temos que calcularmos a . Temos a seguinte equação que relaciona a força magnetomotriz, o fluxo e a relutância:
Nesse circuito, temos duas relutâncias. Logo, a relutância total será a soma da relutância do entreferro com a do núcleo.
Então, substituindo os valores que calculamos:
Passo 5
Então, a será
Como
A corrente será