Exercícios Resolvidos de Introdução aos Circuitos Magnéticos

Exercício 5 1 2 3 4 6 7 8 9 10

Enunciado

Determinar a densidade de fluxo magnético (B ) em cada uma das três pernas do circuito magnético da figura abaixo. Assumir que, dentro do material ferromagnético do núcleo, B é relacionado diretamente com H, através da expressão B = 200 H .

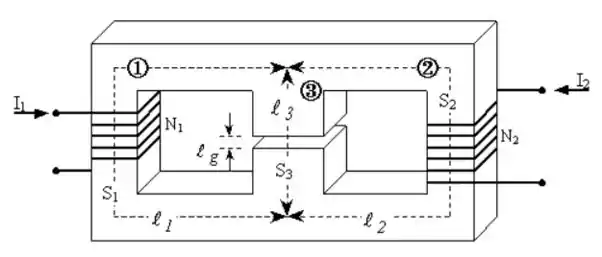
Dados:

Passo 1

Vamos começar desenhando nosso circuito elétrico análogo:

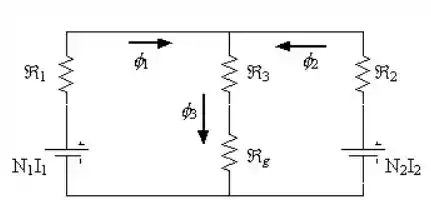
Passo 2

Vamos separar os dados todos pra então fazer os cálculos:

Analisando o circuito análogo vamos chegar nas seguintes equações:

Passo 3

Vamos agora fazer os cálculos das relutâncias:

Para :

Para :

Para :

Para :

Passo 4

Agora, vamos substituir as relutâncias encontradas nas nossas equações do Passo 2 e assim encontraremos os fluxos:

Separamos as equações em:

Agora, substituímos essa última equação em :

Vamos achar e

Passo 5

Por fim, basta calcular as densidades dos fluxos magnéticos:

Para :

Para :

Para :

Resposta

Exercícios de Livros Relacionados

Para o transformador ideal na Figura 13.70b, N 2 / N 1 =10. A razão I 2 / I 1 é:10b) 0.1c) -0.1d)-10

Se o transformador de três enrolamentos estiver conectado conforme representação na Figura 13.71b, o valor da tensão de saída V 0 será:10b) 0.1c) -6d)-10

O transformador ideal na Figura 13.70a tem N 2 / N 1 =10. A razão V 2 / V 1 é:10b) 0.1c) -0.1d)-10

O transformador é usado parar abaixar ou elevar:Tensões CCTensões CATensões CC, bem como CA

Um transformador de três enrolamentos é conectado conforme representação na Figura 13.71a. O valor da tensão se saída V 0 é:10b) 0.1c) -6d)-10