Um núcleo magnético quadrado tem um comprimento médio de e uma área de seção reta de . Uma bobina com espiras é enrolada em torno de uma perna do núcleo. O núcleo é feito de um material cuja curva de magnetização é mostrada abaixo:
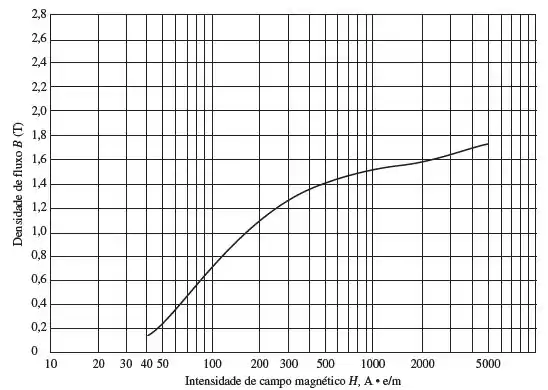
Qual a corrente necessária para produzir de fluxo no núcleo?
Qual a permeabilidade relativa do núcleo nesse nível de corrente?
Qual é a sua relutância?
Passo 1
Primeiro, vamos desenhar o circuito magnético para visualizarmos o problema.
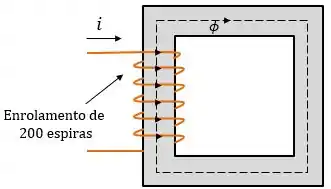
Temos que tomar em relação às unidades. Então, vamos passar tudo o que está em centímetros para metros.
Passo 2
Para encontrarmos a corrente, primeiro temos que calcular a densidade de fluxo no núcleo:
Agora, com o valor calculado, vamos analisamos a curva de magnetização e vemos qual a intensidade de fluxo magnético correspondente a essa densidade.
Passo 3
Pela lei de Ampère podemos relacionar a corrente com a intensidade de campo magnético:
Isolando a corrente:
Substituindo os pelos valores:
Passo 4
A permeabilidade magnética é a propriedade do material em que se encontra o campo magnético que relaciona a intensidade de campo magnético e a densidade de fluxo magnético .
Logo, podemos calculá-la assim:
Como, , a gente determina a permeabilidade relativa fazendo:
Passo 5
Para calcularmos a relutância do núcleo, antes vamos determinar a força magnetomotriz.
Agora é aplicar a fórmula abaixo e correr para o abraço.