Calcule todas as correntes através das resistências pelo método da corrente de malha:
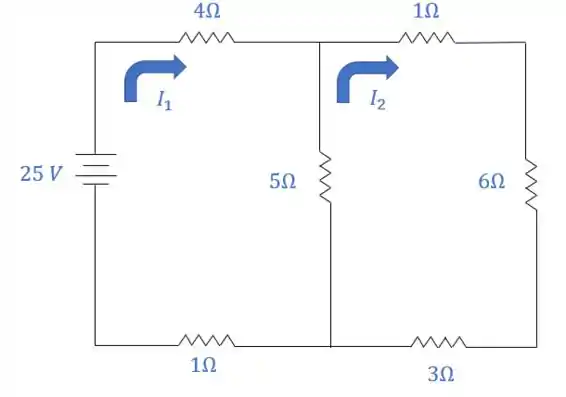
Passo 1
Preparados para mais uma questãozinha de lei de Kirchhoff? Vamo que vamo!
Como ele nos deu as correntes no sentido horário:
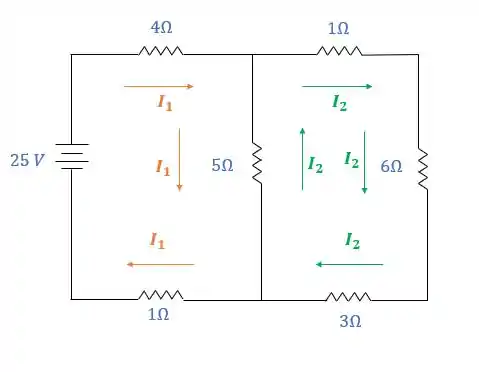
Já somos capazes de estabelecer os polos positivo e negativo de cada queda de tensão, certo?
Lembrando das regrinhas:
- Quando a corrente passa pelo resistor, ela entra pelo polo positivo e sai pelo polo negativo da queda de tensão:
- A fonte de tensão já vem definido o polo positivo e o polo negativo de acordo com seu símbolo:
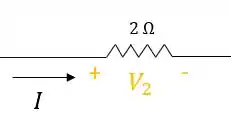
Essa queda de tensão obedece a primeira lei de Ohm
Então, no resistor será igual a:
Vamos definir todos os polos positivos e negativos para o circuito:
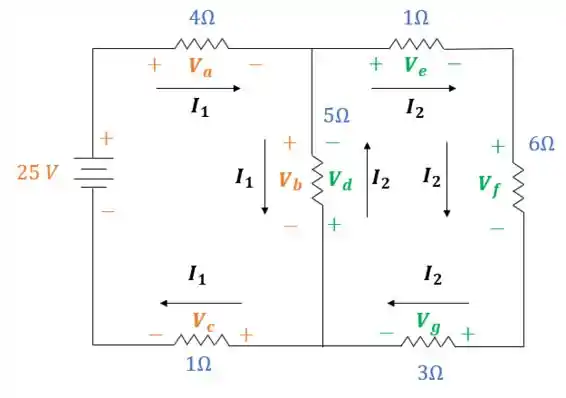
Para facilitar, dividi entre a malha em laranja e a malha em verde!
Passo 2
Vamos calcular as quedas de tensão nos resistores. Utilizaremos a Lei de Ohm:
- Calculando :
- Calculando :
- Calculando :
- Calculando :
- Calculando :
Deixei por último as quedas de tensão e , pois elas estão sob o mesmo resistor de :
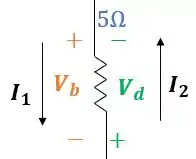
Vamos olhar apenas a queda de tensão e as correntes:
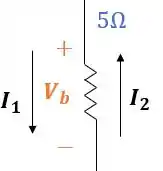
Dessa vez escreveremos a queda de tensão em função das duas correntes:
Veja que eu subtraí de , pois a corrente causa esse posicionamento dos polos positivo e negativo, enquanto se opõe a essa circulação de corrente.
Vamos fazer o mesmo para :
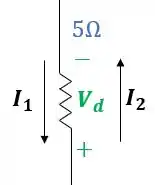
Dessa vez escreveremos a queda de tensão em função das duas correntes:
Passo 3
Vamos aplicar a Lei de Kirchhoff nessas malhas? Olhem de novo para a primeira malha:
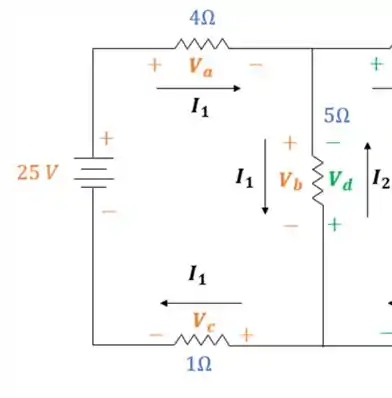
Percorrendo de acordo com a circulação da corrente :
- Fonte de tensão com sinal positivo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
- Queda de tensão com sinal negativo:
Montando a equação para essa malha, temos:
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Vamos substituir as expressões das correntes. As unidades colocaremos só no final, beleza?
Aplicando a distributiva em:
Lembrando que multiplicação entre um número positivo com um número negativo é igual a um número negativo. Porém a multiplicação entre dois números negativos é igual a um número positivo:
Então voltamos para a equação da primeira malha:
Vamos somar todos os termos que são multiplicados por :
Aplicando na equação:
Achamos a primeira relação, vamos guardar ela com carinho! Enquanto isso vamos olhar para a segunda malha!
Passo 4
Vamos olhar de novo para a segunda malha:
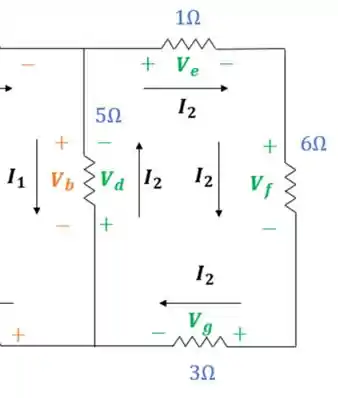
Percorrendo de acordo com a circulação da corrente :
Montando a equação para essa malha, temos:
Pela Lei de Kirchhoff, a soma de todas as tensões e quedas em uma mesma malha deve ser igual a zero!
Vamos substituir as expressões das correntes. As unidades colocaremos só no final, beleza?
Aplicando a distributiva em:
Lembrando que multiplicação entre um número positivo com um número negativo é igual a um número negativo. Porém a multiplicação entre dois números negativos é iguala um número positivo:
Então voltamos para a equação da segunda malha:
Vamos somar todos os termos que são multiplicados por :
Aplicando na equação:
Passando o para o outro lado da equação
Dividindo os dois lados por , ficamos com:
Guardou essa relação? Vamos montar um sistema com as duas relações que encontramos!
Passo 4
As duas relações que encontramos foram:
Se substituirmos a segunda relação na primeira, teremos o seguinte:
Fazendo primeiro essa multiplicação
Voltando para a equação:
Agora vamos passar a corrente para o outro lado
Quando passamos para o outro lado da igualdade, o sinal da corrente ficou positivo!
Dividindo os dois lados por teremos:
UHUL, achamos a segunda corrente!
Vamos encontrar a primeira corrente, substituindo esse valor na relação:
Logo:
Agora ficou fácil de achar a primeira corrente, certo? Estou sentindo que você está entendendo tudo, mas vamos fazer mais exercícios pra melhorar ainda mais!