Um gerador de alimenta o circuito mostrado na figura abaixo, sendo o valor de desconhecido. A diferença de potencial nos terminais do resistor de de . Com estas informações determine o valor de .
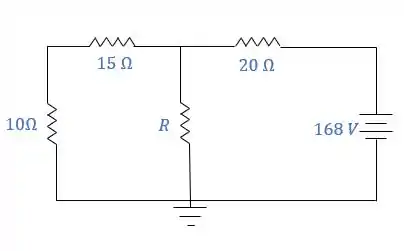
Passo 1
Certo, a primeira informação que o enunciado nos deu é que a queda de tensão em cima do resistor de é igual a :
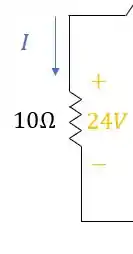
Com essas informações:
Através da Lei de Ohm:
Podemos encontrar o valor da corrente :
Isolando a corrente de um lado da igualdade:
Show, já encontramos a corrente que passa pelo resistor de ! Mas, se olharmos bem o circuito, podemos ver que essa corrente é a mesma que passa pelo resistor de .
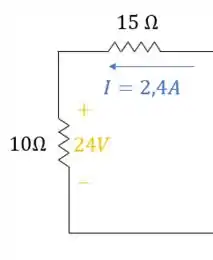
Então já ganhamos essa informação de graça 😊
Passo 2
Assim, utilizando novamente a primeira lei de Ohm
podemos calcular a queda de tensão no resistor de
E aos pouquinhos vamos colhendo informações e expandindo nosso circuito. Vamos continuar!
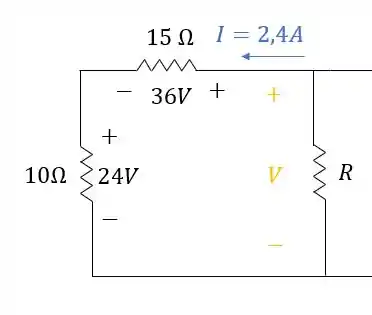
Passo 3
Podemos ver que fechamos uma malha de tensões, pela Lei de Kirchhoff, podemos percorrer a malha no sentido da corrente e encontraremos:
- A queda de tensão sendo negativa:
- A queda de tensão sendo negativa:
- A queda de tensão sendo positiva! Porque os polos da tensão lã do lado direito indicam que o positivo está na parte de cima e o negativo na parte de baixo:
Sabemos que pela Lei de Kirchhoff para tensões, a soma de todas as tensões deve ser igual a zero:
Isolando os números para o outro lado da igualdade, os termos passam de negativo para positivo:
Passo 4
Agora que temos o valor dessa queda de tensão, vamos olhar para a malha com fonte de tensão:
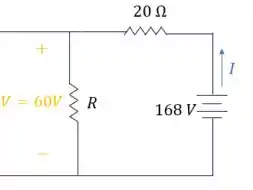
Podemos aplicar novamente a Lei de Kirchhoff, concorda comigo? Para encontrar a queda de tensão em cima do resistor de .
Primeiro passo, vamos destacar os polos positivos e negativos da fonte de tensão e da queda de tensão no resistor de acordo com a corrente:
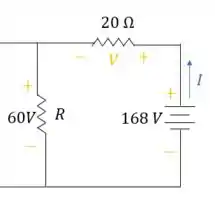
Segundo passo, vamos percorrer a malha seguindo a corrente:
- A fonte de tensão será positiva, pois a corrente entra pelo polo negativo e sai pelo polo positivo:
- A queda de tensão sob o resistor será negativa, pois a corrente entra pelo polo positivo e sai pelo polo negativo:
- A queda de tensão sob o resistor será negativa, pois a corrente entra pelo polo positivo e sai pelo polo negativo:
Montando a equação de acordo com a Lei de Kirchhoff para tensões, sabemos que a soma de todos esses valores de tensão de uma mesma malha deve dar zero:
Passando o termo para o outro lado da igualdade, conseguimos tornar ele positivo:
Realizando essa subtração, encontraremos:
Passo 5
Agora que sabemos sobre a queda de tensão no resistor de , podemos usar a Lei de Ohm para descobrir o valor da corrente que passa por ele:
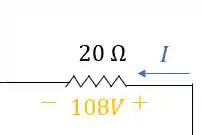
A equação da Lei de Ohm é:
Aplicando os valores que conhecemos:
Vamos isolar a corrente que desejamos encontrar:
Passo 6
Vamos olhar para o nosso circuito, pessoal, com correntes e tensões:
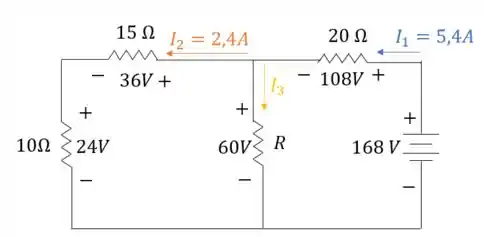
Percebe que sabemos todas as correntes, exceto que está saindo do nó.
Podemos aplicar a Lei de Kirchhoff para correntes, não podemos? Essa Lei nos diz que a soma das correntes que entram no nó é igual a soma das correntes que saem do mesmo nó:
A corrente que entra no nó é apenas , enquanto as correntes que saem do nó são e :
Sabemos os valores:
Isolando a corrente :
Show! Encontramos mais uma informação, mas ainda não terminamos.
Passo 7
Olhe para esse ramo central:
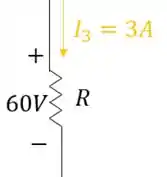
Já sabemos a queda de tensão nesse resistor e a corrente que passa por ele. Para encontrar a resistência podemos aplicar a Lei de Ohm:
Aplicando os valores que já conhecemos da tensão e a corrente
Isolando :
Chegamos na resposta final, pessoal! Demorou, mas chegamos!